标签:
1,题目要求
根据软件工程概论--《环状一维数组最大子数组和》和《二维数组最大子数组和》两篇博客,求环状二维数组的和。
2,思路设计
根据前面两篇博客思路做参考。在二维数组的基础上扩充二维数组的列为2*col-1。再进行二维数组的求和即可。
3,代码
#include <iostream> #include<time.h> using namespace std; #define max(a,b) ((a)>(b)?(a):(b)) #define MAXN 100 int A[MAXN][MAXN]; int PartSum[MAXN][MAXN]; //计算子矩阵的和 int MatrixSum(int s, int t, int i, int j) { return PartSum[i][j] - PartSum[i][t - 1] - PartSum[s - 1][j] + PartSum[s - 1][t - 1]; } int main() { srand((unsigned)time(NULL)); int row, col, i, j; cout << "请输入二维数组的行数和列数:"; cin >> row >> col; for (i = 1; i <= row; i++) { for (j = 1; j <=2* col-1; j++) { for (j = 1; j <= col; j++) { cin >> A[i][j]; } for (j = col + 1; j <= 2 * col - 1; j++) { A[i][j] = A[i][j-col]; } } } for (i = 0; i <= row; i++) PartSum[i][0] = 0; for (j = 0; j <= col; j++) PartSum[0][j] = 0; // 计算矩阵的部分和 for (i = 1; i <= row; i++) for (j = 1; j <= 2*col-1; j++) PartSum[i][j] = A[i][j] + PartSum[i - 1][j] + PartSum[i][j - 1] - PartSum[i - 1][j - 1]; int n1, n2; int maxsofar = A[1][1]; for (n1 = 1; n1 <= row; n1++) for (n2 = n1; n2 <= row; n2++) { // 将子矩阵上下边界设为第n1行和第n2行,在这些子矩阵中取最大值,类似于一维数组求最大值 int maxendinghere = MatrixSum(n1, 1, n2, 1); for (j = 2; j <=2* col-1; j++) { maxendinghere = max(MatrixSum(n1, j, n2, j), MatrixSum(n1, j, n2, j) + maxendinghere); maxsofar = max(maxendinghere, maxsofar); } } cout << maxsofar; }
4,结果截图
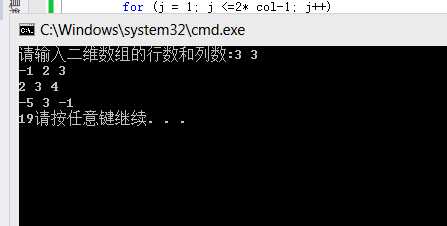
5,总结
技术性不高,就是把二维数组的列数改了一下。重点是复用了以前的程序。从一维数组到二维数组,环状一维数组到环状二维数组。每一步的更新都有前一个程序的思路影子做铺垫。代码的复用和更改是非常简便而适用的。
标签:
原文地址:http://www.cnblogs.com/15732115368zhm/p/4448712.html