标签:
一、设计思路:通过综合求二维数组的最大子数组、求首尾相连的一维数组的最大子数组的算法,得出如下思路:首先将二维数组的子数组上下相加转化成许多一维数组,然后按照求首尾相连的一维数组的算法,遍历一维数组的所有子数组,求出子数组的最大值,即为首尾相连二维数组的子数组的最大值,并且在遍历过程中保留取得最大值的位置,输出二维数组的最大子矩阵。
二、代码:
import java.awt.Point;
import java.util.Scanner;
public class main {
public static int add(int a[][],int i,int j,int k)
{
int n;
int b=0;
for(n=j;n<=i+j;n++)
{
b+=a[n][k];
}
return b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int i,j,k,l;
int sum=0,s,h,e;
Point head=new Point();
Point end=new Point();
Scanner sc=new Scanner(System.in);
System.out.print("请输入矩阵的行数:");
int x=sc.nextInt();
System.out.print("请输入矩阵的列数:");
int y=sc.nextInt();
int a[][]=new int[x][y];
int b[]=new int[y];
System.out.println("请输入数组中的数:");
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
a[i][j]=sc.nextInt();
}
}
for(i=0;i<x;i++)
{
for(j=0;i+j<x;j++)
{
s=0;
h=0;
e=0;
for(k=0;k<y;k++)
{
b[k]=add(a,i,j,k);
}
for(l=0;l<k;l++)
{
s+=b[l];
if(s>0)
{
e++;
}
else
{
s=0;
h=l+1;
e++;
}
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
if(s>0&&h!=0)
{
l=0;
e=e-y;
while(s>0&&e!=h-1)
{
s+=b[l];
l++;
e++;
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
}
}
}
System.out.print("最大子数组的和为:");
System.out.println(sum);
System.out.println("最大子数组为:");
if(end.x>head.x)
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
else
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<y;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
for(j=0;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
}
}
三、结果截图:
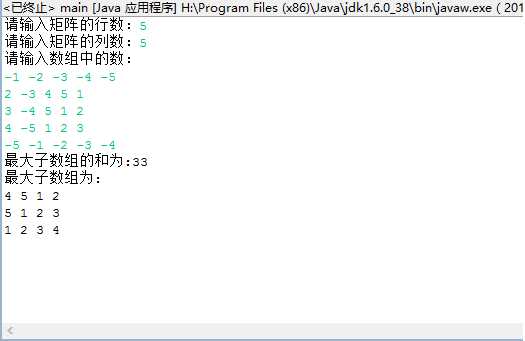
四、总结:本以为这次的程序比较简单,只需要将上两次的程序结合起来,但实际情况并不是如此。在编写过程中,有将原来最大子数组的位置的值由一维变成二维、还有在二维数组转化为一维数组的过程中出现的各种问题。这使我觉得编写程序要亲自动手,才能懂得其中的奥妙,纸上谈兵不可能成功
五、结组开发人员:杜永超、郭昊

标签:
原文地址:http://www.cnblogs.com/act-gh95/p/4451454.html