标签:
一、设计思路:通过综合求二维数组的最大子数组、求首尾相连的一维数组的最大子数组的算法,得出如下思路:首先将二维数组的子数组上下相加转化成许多一维数组,然后按照求首尾相连的一维数组的算法,遍历一维数组的所有子数组,求出子数组的最大值,即为首尾相连二维数组的子数组的最大值,并且在遍历过程中保留取得最大值的位置,输出二维数组的最大子矩阵。
二、代码
import java.awt.Point;
import java.util.Scanner;
public class main {
public static int add(int a[][],int i,int j,int k)
{
int n;
int b=0;
for(n=j;n<=i+j;n++)
{
b+=a[n][k];
}
return b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int i,j,k,l;
int sum=0,s,h,e;
Point head=new Point();
Point end=new Point();
Scanner sc=new Scanner(System.in);
System.out.print("请输入矩阵的行数:");
int x=sc.nextInt();
System.out.print("请输入矩阵的列数:");
int y=sc.nextInt();
int a[][]=new int[x][y];
int b[]=new int[y];
System.out.println("请输入数组中的数:");
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
a[i][j]=sc.nextInt();
}
}
for(i=0;i<x;i++)
{
for(j=0;i+j<x;j++)
{
s=0;
h=0;
e=0;
for(k=0;k<y;k++)
{
b[k]=add(a,i,j,k);
}
for(l=0;l<x;l++)
{
s+=b[l];
if(s>0)
{
e++;
}
else
{
s=0;
h=l+1;
e++;
}
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
if(s>0&&h!=0)
{
l=0;
e=e-x;
while(s>0&&e!=h-1)
{
s+=b[l];
l++;
e++;
if(s>sum)
{
sum=s;
head.x=h;
head.y=j;
end.x=e;
end.y=i+j;
}
}
}
}
}
System.out.print("最大子数组的和为:");
System.out.println(sum);
System.out.println("最大子数组为:");
if(end.x>head.x)
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
else
{
for(i=head.y;i<=end.y;i++)
{
for(j=head.x;j<x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
for(j=0;j<end.x;j++)
{
System.out.print(a[i][j]);
System.out.print(" ");
}
System.out.println();
}
}
}
}
三、结果截图:
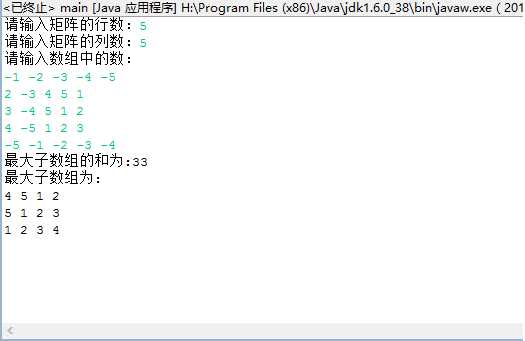
四、总结:总的来说这次开发的过程比较纠结,这次没用到上次那个不是首尾相连的二维数组的程序而是与首尾相连的一维数组算法相似,由于数比较多,在嵌套循环的时候很容易出错,必须要在纸上划清界限然后慢慢的更改,不然的话会造成语言上没错误但是逻辑上很多错误这是比较难检查出来的。本以为运用一维数组的知识会简单但是这个程序远不是感觉得那样,当成功编译出来的时候是很兴奋的。
五、结组开发人员:杜永超、郭昊

标签:
原文地址:http://www.cnblogs.com/dyc940210/p/4451673.html