标签:
查询与排序是使用的再频繁不过的两个功能,算法学习系列实现语言为C#。
Int32 Search(Int32[] source, Int32 task) { var index = 0; while (index < source.Length) if (source[index++] == task) return index - 1; //返回值为Length则说明未找到 return source.Length; }
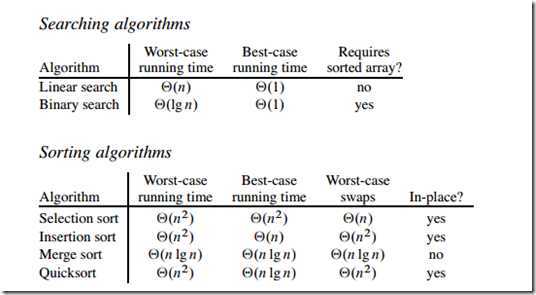
时间复杂度为O(n),在检索源没有排序的情况下,这即为最高的检索方法。
当检索源为顺序排列时,我们可以使用二分查询进行检索。
可将时间复杂度提升至O(lgn).
非递归实现:
Int32 BinarySearch(Int32[] source, Int32 targetVal) { Int32 leftPointer = 0; Int32 rightPointer = source.Length - 1; while (leftPointer <= rightPointer) { Int32 pos = (rightPointer + leftPointer) / 2; if (source[pos] == targetVal) return pos; if (source[pos] < targetVal) leftPointer = pos + 1; else rightPointer = pos - 1; } return source.Length; }
递归实现:
Int32 BinarySearch(Int32[] source, Int32 startIndex, Int32 endIndex, Int32 targetVal) { if (startIndex > endIndex) return source.Length; Int32 pos = (startIndex + endIndex) / 2; if (source[pos] == targetVal) return pos; if (source[pos] < targetVal) return BinarySearch(source, pos + 1, endIndex, targetVal); else return BinarySearch(source, startIndex, pos - 1, targetVal); }
测试结果:
//输出均为8 Console.WriteLine(BinarySearch(new Int32[10] { 4, 3, 2, 1, 3, 8, 9, 19, 88, 57 }, 0, 10, 88)); Console.WriteLine(BinarySearch(new Int32[10] { 4, 3, 2, 1, 3, 8, 9, 19, 88, 57 }, 88));
接下来是一些常用的排序方法。
时间复杂度O(n*n)。
Int32[] SelectionSort(Int32[] source) { for (int i = 0; i < source.Length; i++) { var smallestValIndex = i; for (int j = i + 1; j < source.Length; j++) { if (source[smallestValIndex] > source[j]) smallestValIndex = j; } var temp = source[i]; source[i] = source[smallestValIndex]; source[smallestValIndex] = temp; } return source; }
时间复杂度O(n*n),与选择法相比,适合在链表结构中使用。
Int32[] InsertSort(Int32[] source) { var resultArray = new Int32[source.Length]; for (int i = 0; i < source.Length; i++) { var index = 0; while (index++ < i) { if (resultArray[index - 1] > source[i]) break; } for (int j = index - 1; j < i; j++) resultArray[j + 1] = resultArray[j]; resultArray[index - 1] = source[i]; } return resultArray; }
时间复杂度O(n * lgn)。
分治原理例图:
Int32[] DevideAndConquerSort(Int32[] source, Int32 startIndex, Int32 endIndex) { //子数组只有一个元素时,是无需排序的 if (startIndex + 1>= endIndex) return source; var middleIndex = (startIndex + endIndex) / 2; DevideAndConquerSort(source, startIndex, middleIndex); DevideAndConquerSort(source, (startIndex + endIndex) / 2, endIndex); MergeSort(source, startIndex, (startIndex + endIndex) / 2, endIndex); return source; } void MergeSort(Int32[] source, Int32 startIndex, Int32 middleIndex, Int32 endIndex) { var arrayAPointer = startIndex; var arrayBPointer = middleIndex; var loopLength = endIndex - startIndex; var resultArray = new Int32[loopLength]; for (int i = 0; i < loopLength; i++) { if (arrayBPointer != endIndex && source[arrayAPointer] > source[arrayBPointer]) resultArray[i] = source[arrayBPointer++]; else if (arrayAPointer != middleIndex) resultArray[i] = source[arrayAPointer++]; else resultArray[i] = source[arrayBPointer++]; } for (int i = 0; i < loopLength; i++) { source[startIndex + i] = resultArray[i]; } }
与合并法相比,适合在n不是很大,又不是很小的时候使用。
分治原理例图:
Int32[] QuickSort(Int32[] source, Int32 startIndex, Int32 endIndex) { if(startIndex >= endIndex) return source; var index = Partition(source, startIndex, endIndex); QuickSort(source, startIndex, index - 1); QuickSort(source, index + 1, endIndex); return source; } Int32 Partition(Int32[] source, Int32 startIndex, Int32 endIndex) { Int32 index = 0; while ((index++) < endIndex - startIndex) { if (source[startIndex + index - 1] >= source[endIndex - 1]) break; } if(startIndex + index - 1 != endIndex) { var temp = source[startIndex + index - 1]; source[startIndex + index - 1] = source[endIndex - 1]; source[endIndex - 1] = temp; } return startIndex + index - 1; }
标签:
原文地址:http://www.cnblogs.com/E-WALKER/p/4458087.html