There is an infinite sequence consisting of all positive integers in the increasing order: p?=?{1,?2,?3,?...}. We performed n swapoperations with this sequence. A swap(a,?b) is an operation of swapping the elements of the sequence on positions a and b. Your task is to find the number of inversions in the resulting sequence, i.e. the number of such index pairs (i,?j), that i?<?j and pi?>?pj.
The first line contains a single integer n (1?≤?n?≤?105) — the number of swap operations applied to the sequence.
Each of the next n lines contains two integers ai and bi (1?≤?ai,?bi?≤?109, ai?≠?bi) — the arguments of the swap operation.
Print a single integer — the number of inversions in the resulting sequence.
2 4 2 1 4
4
3 1 6 3 4 2 5
15
In the first sample the sequence is being modified as follows: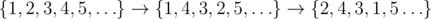 
.
It has 4 inversions formed by index pairs (1,?4), (2,?3), (2,?4) and (3,?4).
题意：一个1,2,3,4,....的序列（长度无限)进行n次操作每次操作交换位置a和b上的数，问最终的序列有多少对逆序数。
先用map搞出最终的序列(只需要搞出题目中交换位置的数就行)。然后按照树状数组求逆序对的方式来操作。不过需要进行一下离散化。
考虑这样一个序列a[l],l+1,l+2,....,r-1,a[r]其中l和r上的数是交换过的（不一定是l和r上的进行交换），考虑中间那段对逆序数的影响，令w = (r-1)- (l+1)-1，右边小于l+1的数为x，则右边的数对这段区间[l+1,r-1]逆序数的贡献是w*x(所以ans += w*Query(Loc-1)),这段区间对在l+1左边且值大于r-1的每个数贡献也是w(所以Modify(Loc-1,w,tot))
#include <bits/stdc++.h>
#define foreach(it,v) for(__typeof((v).begin()) it = (v).begin(); it != (v).end(); ++it)
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 100;
ll c[maxn];
#define lowbit(x) (x)&(-x)
void Modify(int x,ll d,int n)
{
while(x<=n) {
c[x] += d;
x += lowbit(x);
}
}
ll Query(int x)
{
ll res = 0;
while(x>0) {
res += c[x];
x -= lowbit(x);
}
return res;
}
int main(int argc, char const *argv[])
{
int n;
while(cin>>n) {
map<int,int>Q;
for(int i = 0; i < n; i++) {
int L,R; cin>>L>>R;
if(Q.find(L)==Q.end())Q[L] = L;
if(Q.find(R)==Q.end())Q[R] = R;
swap(Q[L],Q[R]);
}
int tot = 0;
vector<pair<int,int> >v;
vector<int> sec;
foreach(it,Q) {
v.push_back(*it);
sec.push_back(it->second);
tot++;
}
sort(sec.begin(), sec.end());
memset(c,0,sizeof(c[0])*(tot+10));
ll ans = 0;
for(int i = tot-1; i >= 0; i--) {
int Loc = lower_bound(sec.begin(), sec.end(),v[i].second)-sec.begin() + 1;
ans += Query(Loc-1);/*统计右边小于v[i].second的数*/
if(i==0)break;
Modify(Loc,1,tot);
ll w = (v[i].first-1) - v[i-1].first;/*a[l],l+1,l+2,...r-1,a[r]中的[l+1,r-1]区间元素个数*/
if(w<1)continue;
Loc = lower_bound(sec.begin(), sec.end(),v[i-1].first+1)-sec.begin()+1;/*序列v[i-1].first+1,v[i-1].first+2...,v[i].first-1在离散化后的位置*/
ans += w*Query(Loc-1);/*统计序列v[i-1].first+1,v[i-1].first+2...,v[i].first-1右边小于该序列的数*/
/*为什么要在Loc-1加上w呢因为v[i].first离散出来的位置是Loc，如果此处是Loc且v[k].second==v[i].first的k小于i，
那么统计v[k].first这个位置的逆序数时不会统计到这段连续的区间*/
Modify(Loc-1,w,tot);
}
cout<<ans<<endl;
}
return 0;
}Codeforces Round #301 (Div. 2)（树状数组+离散化）
原文地址：http://blog.csdn.net/acvcla/article/details/45466497
