堆排序

1.堆的概念
参考：http://www.cnblogs.com/luchen927/archive/2012/03/08/2381446.html
堆（heap),一种数据结构，堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。
或者说，堆排序将所有的待排序数据分为两部分，无序区和有序区。无序区也就是前面的最大堆数据，有序区是每次将堆顶元素放到最后排列而成的序列。每一次堆排序过程都是有序区元素个数增加，无序区元素个数减少的过程。当无序区元素个数为1时，堆排序就完成了。
本质上讲，堆排序是一种选择排序，每次都选择堆中最大的元素进行排序。只不过堆排序选择元素的方法更为先进，时间复杂度更低，效率更高。
堆排序过程
堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。
既然是堆排序，自然需要先建立一个堆，而建堆的核心内容是调整堆，使二叉树满足堆的定义（每个节点的值都不大于其父节点的值）。调堆的过程应该从最后一个非叶子节点开始，假设有数组A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么调堆的过程如下图，数组下标从0开始，A[3] = 5开始。分别与左孩子和右孩子比较大小，如果A[3]最大，则不用调整，否则和孩子中的值最大的一个交换位置，在图1中是A[7] > A[3] > A[8]，所以A[3]与A[7]对换，从图1.1转到图1.2。

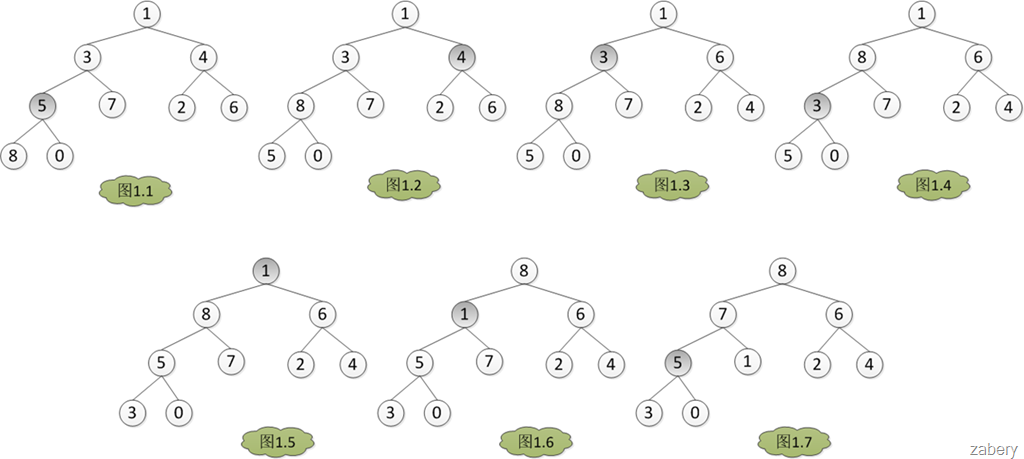
调堆：如果初始数组是非降序排序，那么就不需要调堆，直接就满足堆的定义，此为最好情况，运行时间为Θ(1)；如果初始数组是如图1.5，只有A[0] = 1不满足堆的定义，经过与子节点的比较调整到图1.6，但是图1.6仍然不满足堆的定义，所以要递归调整，一直到满足堆的定义或者到堆底为止。如果递归调堆到堆底才结束，那么是最坏情况，运行时间为O(h) (h为需要调整的节点的高度，堆底高度为0，堆顶高度为floor(logn) )。

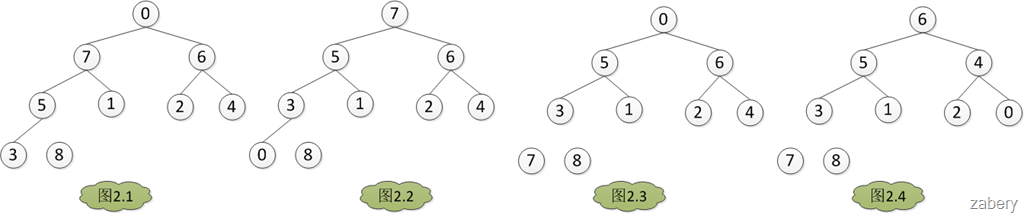
建堆完成之后，堆如图1.7是个大根堆。将A[0] = 8 与 A[heapLen-1]交换,然后heapLen减一，如图2.1，然后AdjustHeap(A, heapLen-1, 0)，如图2.2。如此交换堆的第一个元

素和堆的最后一个元素，然后堆的大小heapLen减一，对堆的大小为heapLen的堆进行调堆，如此循环，直到heapLen == 1时停止，最后得出结果如图3。

2.堆的性质维护
2．二叉堆性质维护问题描述
?
输入：数组A[1…n]存储的一棵几乎完全二叉树，正整数i。其中以A[i]为根的子树中，A[i]的两个孩子已构成最大堆。
?
输出：数组A。其中，以A[i]为根的子树中的节点布局有所变动构成最大堆。
2.1 堆性质维护算法的伪代码描述

MAX-HEAPIFY(A, i)//运行时间(lgn)
1 l ← LEFT(i)
2 r ← RIGHT(i)
3 if l ≤ heap-size[A] and A[l] > A[i]
4 then largest ← l
5 else largest ← i
6 if r ≤ heap-size[A] and A[r] > A[largest]
7 then largest ← r
8 if largest ≠ i
9 then exchange A[i] ? A[largest]
10 MAX-HEAPIFY(A, largest)

3.二叉堆创建问题描述
?输入：数组A[1…n]。
?输出：重排后的数组A[1…n]，元素间构成一个堆。
3.1 创建堆算法的伪代码描述
利用过程MAX-HEAPIFY以自底向上的方式将数组A[1……n]转换为一个最大堆。由于子数组A[[n/2]+1…..n]的每一个元素都没有左右孩子，所以都是树的叶子，因此每一个觉构成一个单元素堆。过程BUILD-MAX-HEAP检测树中的其余节点并对每个节点运行MAX-HEAPIFY。

BUILD-MAX-HEAP(A)
1 heap-size[A] ← length[A]
2 for i ← ?length[A]/2? downto 1
3 do MAX-HEAPIFY(A, i)

BUILD-MAX-HEAP运行的一个例子：

堆创建算法的运行时间：o(nlgn).
4 程序实现
4.1(C语版本）

#include <stdlib
#include "heap.h"
#include "swap.h"
/**************堆排序相关算法********************/
// i:给定的节点下标

int left(int i)//左孩子下标
{
return 2 * i + 1;
}
int right(int i)//右孩子下标
{
return 2 * i + 2;
}
int parent(int i)//父节点下标
{
return (i - 1) / 2;
}
/***************************
函数：heapify
功能：堆性质维护
输入参数：a :序列数组
size:数据类型所占字节
i:待维护节点下标
heapsize:堆中元素个数
*comp:比较函数，以便实现最大堆和最小堆的通用算法

****************************/
void heapify(void *a, int size, int i, int heapsize, int(*comp)(void*, void*))
{
int l = left(i), r = right(i), most;//most: A[I],A[l],A[r]中的最大或最小
if (l < heapsize&&comp((char*)a + l*size, (char*)a + i*size)>0)//l<heapsize且A[i]<A[l]
most = l;//根节点大于左孩子
else
most = i;
if (r < heapsize&&comp((char*)a + r*size, (char*)a + most*size)>0)//r<heapsize且A[r]>A[most]
most = r;

if (most != i)//i不是最大或最小节点，则元素位置调换，使其 满足堆的性质
{
swap((char*)a + i*size, (char*)a + most*size, size);
heapify(a, size, most, heapsize, comp);//递归检测
}
}
/***************************
函数：buildHeap
功能：建堆
输入参数：a :序列数组
size:数据类型所占字节
length:数组中元素个数
*comp:比较函数，以便实现最大堆和最小堆的通用算法

****************************/
void buildHeap(void*a, int size, int length, int(*comp)(void*, void*))
{
int i;//循环控制变量循环检测节点性质并维护
for (i = (length / 2) - 1; i >= 0; i--)
heapify(a, size, i, length, comp);
}

#include <stdio.h>
#include <stdlib.h>
#include"compare.h"
#include "sort.h"
#include"merge.h"
#include "partition.h"
#include "heap.h"
int main(int argc, char** argv)
{
    int b[] = { 4,1,3,2,16,9,10,14,8,7 }, i;
    buildHeap(b, sizeof(int),10, intGreater);
    printf("max heap:\n");
    for (i = 0; i < 10; i++)
        printf("%d  ", b[i]);
    printf("\n");
    buildHeap(b, sizeof(int), 10, intLess);
    printf("min heap:\n");
    for (i = 0; i < 10; i++)
        printf("%d  ", b[i]);
    printf("\n");
    system("pause");
    return EXIT_SUCCESS;
}

4.2 （C++版)

#ifndef _HEAP_H
#define _HEAP_H

int left(int i)
{
    return 2 * i + 1;
}
int right(int i)
{
    return 2 * i + 2;
}
int parent(int i)
{
    return (i - 1) / 2;
}
template<typename Iterator,typename Comparator>
void heapify(Iterator _first, Iterator _last, int i, Comparator comp)
{
    int l = left(i), r = right(i), most;
    int n = distance(_first, _last);
    if (l < n&&comp(*(_first + l), *(_first + i))>0)
        most = l;
    else
        most = i;
    if (r < n&&comp(*(_first + r), *(_first + most))>0)
        most = r;
    if (most!=i)
    {
        iter_swap(_first + i, _first + most);
        heapify(_first, _last, most, comp);
    }
}
template<typename Iterator,typename Comparator>
void buildHeap(Iterator _first, Iterator _last, Comparator comp)
{
    int n=distance(_first,_last),i;
    for (i = n / 2 - 1; i >= 0;i--)
    {
        heapify(_first, _last, i, comp);
    }
}
#endif

#include "stdafx.h"
#include<string.h>
#include <stdlib.h>
#include <vector>
#include <iterator>
#include <iostream>
#include<algorithm>
#include <functional>//定义运算函数（代替运算符）
#include "heap.h"
using namespace std;
int main(int argc, _TCHAR* argv[])
{
int a[]={4,1,3,2,16,9,10,14,8,7};
vector<int> va = vector<int>(a, a + 10);//用数组创建vector对象
buildHeap(va.begin(), va.end(), greater<int>());
cout << "max heap:" << endl;
copy(va.begin(), va.end(), ostream_iterator<int>(cout, " "));
buildHeap(va.begin(), va.end(), less<int>());
cout << endl;
cout << "min heap:" << endl;
copy(va.begin(), va.end(), ostream_iterator<int>(cout, " "));
//make_heap(va.begin(),va.end(),greater<int());//STL 堆操作函数
//copy(va.begin(), va.end(), ostream_iterator<int>(cout, " "));
system("pause");
return 0;
}

运行结果：