标签：
EM算法，之前上模式识别课上，推导过，在《统计学习方法》中没耐性的看过几次，个人感觉讲的过于理论，当时没怎么看懂，后来学lda，想要自己实现一下em算法，又忘记了，看来还是学的不够仔细，认识的不够深刻，现在做点笔记。本文是看了几篇blog和《统计学习方法》之后做的笔记，只是用来给自己做记录，很多地方都是直接引用。
一、初识
1. 迭代
EM算法本身可以理解为一个迭代算法，很抽象&简单的形容迭代就是，比如我们有两个公式a=f(b), b=g(a)，需要求解，我们可以先随机的给a赋一个值，在根据b=g(a)计算出b，得到b，在根据b得到a，如此往复，直到a，b基本不变。
2. 隐变量问题
EM算法很适用与求解包含隐变量的问题，这里引用《统计学习方法》中的一个例子（pLSA的弱化版本）：
eg. 有3枚硬币，分别记为A，B，C，掷得正面的概率分别为∏，p，q；
先投掷硬币A，如果是正面则继续投掷硬币B，是反面则投掷硬币C，最终出现正面记为1，出现反面记为0；
独立的重复n次实验后，得到一串实验结果Y=(Y1,Y2,……,Yn)。
这里Y=(Y1,Y2,……,Yn)T称作观测变量，但这里也有不能直接观测到，但却需要知道的一个变量，即投掷A的结果，可以记为Z=(Z1,Z2,……,Zn)T，同时有些已知的参数，我们可以统一记为θ=(∏, p, q)。通过上面的一些符号，我们可以得知Y的分布：
上式即为Y的似然函数，得到了似然函数，第一想到的便是参数的似然估计 ，下面回顾一下最大似然估计（MLE）的一般步骤：
求最大似然函数估计值的一般步骤： （1）写出似然函数； （2）对似然函数取对数，并整理； （3）求导数，令导数为0，得到似然方程； （4）解似然方程，得到的参数即为所求
其实最大似然可以这样想，我们假设已经知道到了θ，在已知θ的情况下，产生Y，很自然，如果我们看到结果产生了很多个Yi，那么P(Yi|θ)一定是比较大的。现在我们反过来想，我们已经知道了Y，
，那么使该结果出现的可能性最大的参数情况，就是我们估计的参数。
很不巧，上述步骤，是没有解析解的，这样我们就必须用到EM算法了。
3. Jensen不等式
回顾优化理论中的一些概念。设f是定义域为实数的函数，如果对于所有的实数x，
，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（
），那么f是凸函数。如果
或者
，那么称f是严格凸函数。
Jensen不等式表述如下：
如果f是凸函数，X是随机变量，那么
特别地，如果f是严格凸函数，那么
当且仅当
，也就是说X是常量。
如果用图表示会很清晰：
图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到
成立。
当f是（严格）凹函数当且仅当-f是（严格）凸函数。
Jensen不等式应用于凹函数时，不等号方向反向，也就是
。
二、EM算法
上面的例子，有个很悬乎的变量，我们无法直接知道，即A硬币的投掷结果，但如果我们知道了某一次输出在投掷A后的输出是什么了，我们就能够很容易运用最大似然（当然，这个例子用简单的直觉也能知道）得到p，q的估计值。
eg.
1.如果A硬币的投掷结果有x次正面，n-x次反面（在这个假设下，也就得到了∏的估计值），那么我们只要统计那x次中最后出现的正反面情况就能得到p的估计值了，对q也同理；
2.得到了p，q值之后，我们又容易反过来问，你怎么知道之前的假设是正确的呢？而在已知p，q的情况下，之前我们的似然函数就能够求解了，这样我们就又能得到一个新的∏
3.在新的∏值下，我们又可以对p，q进行新的估计了。如此往复，如果最终收敛了，那么就得到了我们对参数θ的估计值
上面说的很抽象，下面具体地说一说（以下部分引自（EM算法）The EM Algorithm）。
给定的训练样本是
，样例间独立，那么样本的似然函数如下：
第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和（对z求和后即可得到x的边缘分布概率）。但是直接求θ一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化
，我们可以不断地建立
的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。
对于每一个样例i，让
表示该样例隐含变量z的某种分布，
满足的条件是
。（如果z是连续性的，那么
是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了（上文提到的三个硬币的例子中的∏就可以理解为这里的，对于每个i，都是∏，∏是伯努利分布）。
可以由前面阐述的内容得到下面的公式：
（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。
（2）到（3）利用了Jensen不等式。
考虑到
是凹函数（二阶导数小于0），而且
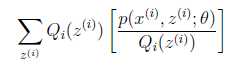，可以理解为
的期望。得到(3)式后，我可以理解为，得到了似然函数l(θ)的一个下界，如果不断提升下界，使下界的值与l(θ)近似相等时，我们就可以用不等式右边的值代替l(θ)了。
对于
的选择，有多种可能，那种更好的？假设
已经给定，那么
的值就决定于
和（其实应该是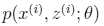
，但这里只有未知）。首先我们思考当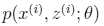和都已经确定时，也就是jensen不等式中的随机变量已知时，我们可以知道当该随机变量恒为常数时，不等式取等号，即：
c为常数，不依赖于
（但确是依赖于x(i)的，所以对于不同i，c还是不一样的，但都是常数）。对此式子做进一步推导，我们知道
，那么也就有
，那么有下式：
至此，我们推出了在固定其他参数
后，
的计算公式就是后验概率，解决了
如何选择的问题。这一步就是E步，建立
的下界。接下来的M步，就是在给定
后，调整
，去极大化
的下界（在固定
后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：
|
循环重复直到收敛 { （E步）对于每一个i，计算 （M步）计算
|
那么如何证明EM算法会收敛，其实有下面公式就好了：
这里证明了
，即l(θ)是单调上升的，到最后就一定能收敛到最大值。具体解释：
（4）是对所有的参数都满足，而其等式成立条件只是在固定
，并调整好Q时成立（即如果是，等式成立），这里
不一定等于
，所以不一定能取等号。
（4）到（5）就是M步的定义，是固定第t步，固定Q调整
得到的结果
（5）到（6）是前面E步所保证等式成立条件。
也就是说E步会将下界拉到与
一个特定值
（这里
）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与
另外一个特定值一样的高度，即此时下界还是要小于
，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到将下界拉升到的最大值。
某 blog 中有个很形象的图，引用到这里
如果定义
从前面的推导中我们知道
，EM可以看作是J的坐标上升法，E步固定
，优化
，M步固定
优化
。
EM算法的基本原理就是这些了
Reference
1. 统计学习方法
2. http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
3. http://blog.csdn.net/zouxy09/article/details/8537620
4. Andrew Ng 课程
Expectation Maximization（EM）算法note
标签：
原文地址：http://www.cnblogs.com/celia01/p/4488711.html
