一、前言

在统计计算中，最大期望（EM）算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（Data Clustering）领域。

最大期望算法经过两个步骤交替进行计算，第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；第二步是最大化（M），最大化在 E 步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

其应用在机器学习算法包括KMeans算法、GMM算法等等，通俗来说，是一种参数初始化，不断迭代寻求较优参数的方法。

二、EM算法推导

2.1 对数似然函数

假设我们有一个样本集{x(1),…,x(m)}，包含m个独立的样本。但每个样本i对应的类别z(i)是未知的（相当于聚类，联系一下KMeans），也即隐含变量，故我们需要估计概率模型p(x,z)的参数θ，但是由于里面包含隐含变量z，所以很难用最大似然求解。

也就是说我们的目标是找到适合的θ和z让L(θ)最大。那我们也许会想，你就是多了一个未知的变量而已啊，我也可以分别对未知的θ和z分别求偏导，再令其等于0，求解出来不也一样吗？本质上这样是可以的，但利用Jensen不等式我们绕开了两个变量求偏导的方式，转而利用通过一个变量最大化函数下界（其实本质也可能是求导）与求一个变量导数相结合的方法。有公式：

其中（2）式到（3）的转换就是利用了Jensen不等式。

2.2 Jensen不等式

2.2.1 为什么不求偏导

本质上我们是需要最大化（1）式（对（1）式，我们回忆下联合概率密度下某个变量的边缘概率密度函数的求解，注意这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和，也就得到等式左边为随机变量x的边缘概率密度），也就是似然函数，但是可以看到里面有“和的对数”，求导后形式会非常复杂（自己可以想象下log(f1(x)+ f2(x)+ f3(x)+…)复合函数的求导），所以很难求解得到未知参数z和θ。那OK，我们可否对（1）式做一些改变呢？我们看（2）式，（2）式只是分子分母同乘以一个相等的函数，还是有“和的对数”啊，还是求解不了，那为什么要这么做呢？咱们先不管，看（3）式，发现（3）式变成了“对数的和”，那这样求导就容易了。我们注意点，还发现等号变成了不等号，为什么能这么变呢？这就是Jensen不等式的大显神威的地方。且看下面推导。

2.2.2 Jensen不等式

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数。

Jensen不等式表述如下：

• 如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])
• 特别地，如果f是严格凸函数，当且仅当X是常量时，上式取等号。

图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。

Jensen不等式应用于凹函数时，不等号方向反向，上述的（2）式到（3）式就是凹函数。
回到公式（2），详细推导如下：

凹函数：E[f(x)]>=f(E(x))
在这里，
X=，

E(x)=

f(x)=log(x)
则：

到这里，现在式（3）就容易地求导了，但是式（2）和式（3）是不等号啊，式（2）的最大值不是式（3）的最大值啊，而我们想得到式（2）的最大值，那怎么办呢？

现在我们就需要一点想象力了，上面的式（2）和式（3）不等式可以写成：似然函数L(θ)>=J(z,Q)，那么我们可以通过不断的最大化这个下界J，来使得L(θ)不断提高，最终达到它的最大值。

见上图，我们固定θ，调整Q(z)使下界J(z,Q)上升至与L(θ)在此点θ处相等（绿色曲线到蓝色曲线），然后固定Q(z)，调整θ使下界J(z,Q)达到最大值（θt到θt+1），然后再固定θ，调整Q(z)……直到收敛到似然函数L(θ)的最大值处的θ*。这里有两个问题：什么时候下界J(z,Q)与L(θ)在此点θ处相等？为什么一定会收敛？

首先第一个问题（回答第二个问题看2.3），在Jensen不等式中说到，当自变量X是常数的时候，等式成立。而在这里，即：

因为Q是随机变量z(i)的概率密度函数，则可以得到：分子的和等于c（分子分母都对所有z(i)求和：多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），则：

至此，我们推出了在固定参数θ后，使下界拉升的Q(z)的计算公式就是后验概率，解决了Q(z)如何选择的问题。这一步就是E步，建立L(θ)的下界，也就是不等式的作用所在。接下来的M步，就是在给定Q(z)后，调整θ，去极大化L(θ)的下界J（在固定Q(z)后，下界还可以调整的更大）。

2.3 EM算法概述

期望最大算法是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。

EM的算法流程：

• 初始化分布参数θ；
• 重复以下步骤直到收敛：
  E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值：
  
  M步骤：将似然函数最大化以获得新的参数值
  

说说M步骤，回答为什么会收敛：

这个不断的迭代，就可以得到使似然函数L(θ)最大化的参数θ了。那就得回答刚才的第二个问题了，它会收敛吗？

感性的说，因为下界不断提高，所以极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。理性分析的话，就会得到下面的东西：

博客中提到这个怎么来的：

第（4）步得到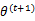时，只是最大化，也就是的下界，而没有使等式成立，等式成立只有是在固定θ，并按E步得到Qi时才能成立。

况且根据我们前面得到的下式，对于所有的Qi和θ都成立

第（5）步利用了M步的定义，M步就是将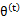调整到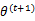，使得下界最大化。因此（5）成立，（6）是之前的等式结果。

这样就证明了会单调增加。一种收敛方法是不再变化，还有一种就是变化幅度很小。

再次解释一下（4）、（5）、（6）。首先（4）对所有的参数都满足，而其等式成立条件只是在固定θ，并调整好Q时成立，而第（5）步只是固定Q，调整θ，不能保证等式一定成立。（4）到（5）就是M步的定义，（5）到（6）是前面E步所保证等式成立条件。也就是说E步会将下界拉到与一个特定值（这里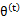）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与另外一个特定值一样的高度，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到最大值。

总体来说：

• 从（2）到（3）取“=”就是“通过一个变量最大化函数下界”的步骤，即E步，联想一下KMeans中取各个类数据的均值作为质心这个步骤，就是在数据属于某个类的情况下（固定一个变量）最大化某个概率。
• 而固定z或说Q(z)，使（3）式数值变大就是“求一个变量导数”的步骤，即M步。

本文参考以下优秀博文并理清一些逻辑：
http://blog.csdn.net/zouxy09/article/details/8537620
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

有些东西还是讲得有些抽象，但相信不断地深入学习和应用到实际场景应该就有所领悟，共勉。