标签:
1 24点简介
拿一副牌,抽去大小王后(初练也可以把J/Q/K也拿去),剩下1~10这40张牌(以下用1代替A)。任意抽取4张牌(称为牌组),用加、减、乘、除 (可加括号)把牌面上的数算成24。每张牌必须且只能用一次。如抽出的牌是3、8、8、9,那么算式为(9-8)×8×3=24。
解决本问题两种常见思路:
1. 表达式加括号。可以选择:不加括号,1个括号,2个括号。
2. 逆波兰表达式。
2 逆波兰表达式
逆波兰表达式又叫做后缀表达式。在通常的表达式中,二元运算符总是置于与之相关的两个运算对象之间,这种表示法也称为中缀表示。波兰逻辑学家J.Lukasiewicz于1929年提出了另一种表示表达式的方法,按此方法,每一运算符都置于其运算对象之后,故称为后缀表示。
2.1 解释
逆波兰记法中,操作符置于操作数的后面。例如表达“三加四”时,写作“3 4 +”,而不是“3 + 4”。如果有多个操作符,操作符置于第二个操作数的后面,所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 +”:先3减去4,再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 * 5”与“(3 - 4)*5”不相同,但后缀记法中前者写做“3 4 5 * -”,无歧义地表示“3 (4 5 *) −”;后者写做“3 4 - 5 *”。
逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是:操作数入栈;遇到操作符时,操作数出栈,求值,将结果入栈;当一遍后,栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现,和能很快求值。
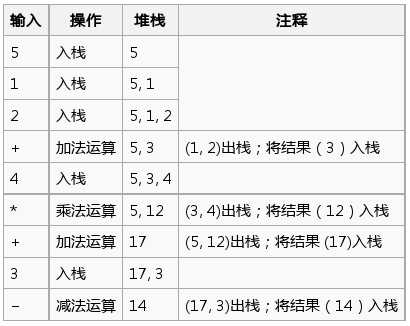
中缀表达式“5 + ((1 + 2) * 4) − 3”写作
下表给出了该逆波兰表达式从左至右求值的过程,堆栈栏给出了中间值,用于跟踪算法。
1 # --rpn.py-- 2 from itertools import permutations # 全排列 3 from fractions import Fraction # 分数运算 4 from operator omport add, sub, mul, div # 函数+ - × / 5 6 card = map(str, [5, 5, 5, 1]) # 输入4张牌存为字符 7 dict_op = {‘+‘: add, ‘-‘:sub, ‘*‘:mul, ‘/‘:div} # 将运算符转为调用函数 8 op = [‘+‘, ‘-‘, ‘*‘, ‘/‘] * 3 # 四则运算,4张牌需要3次运算 9 op1 = list(permutations(op, 3)) # op中任取三个做全排列,结果构成列表 10 op2 = map(lambda x: list(x), op1) # 列表元素从元组转为列表 11 op3 = map(lambda x: sorted(x), op2) # 排序 12 ops = set(map(lambda x: tuple(x), op3)) # 列表转为集合,去重 13 14 # 逆波兰表达式实现 15 def rpn(lst): 16 stack = [] # 初始化栈 17 for i in lst: # 遍历传入表达式列表 18 if i.isdigit(): # 若为数字,则直接进栈 19 stack.append(Fraction(i.strip())) 20 else: 21 if i in dict_op: # 若为运算符,则取出两元素作运算 22 try: 23 a = stack.pop() 24 b = stack.pop() 25 stack.append(dict_op(b, a)) 26 except: break 27 if len(stack) == 1: # 若最后栈内剩余一个元素,接将结果输出 28 return stack[0] 29 30 # 计算24 31 for operator in ops: # 遍历每一种运算符组合 32 space = [] 33 space = card + list(operator) # 组合卡牌和运算符 34 s = set(permutations(space)) # 排列卡牌运算符所有可能 35 for j in s: 36 if rpn(list(j)) == 24: 37 print j 38 39 print ‘Game over‘
标签:
原文地址:http://www.cnblogs.com/freyr/p/4493773.html