标签:
直接选择排序是程序里面非常基础的一个排序算法,算法效率不高,但相对很稳定。
算法原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
示例数据:比如有如下数组 R[] 和每一次计算的结果
1 int R[] = { 5 ,7 ,8 ,0 ,2 ,6 }; 2 3 //第一次结果 4 { 5 ,7 ,8 ,0 ,2 ,6 } 0 ==> { 0 ,7 ,8 ,5 ,2 ,6 }; 5 6 //第二次结果 7 { 0 ,7 ,8 ,5 ,2 ,6 } 2 ==> { 0 ,2 ,8 ,5 ,7 ,6 }; 8 9 //第三次结果 10 { 0 ,2 ,8 ,5 ,7 ,6 } 5 ==> { 0 ,2 ,5 ,8 ,7 ,6 }; 11 12 //第四次结果 13 { 0 ,2 ,5 ,8 ,7 ,6 } 6 ==> { 0 ,2 ,5 ,6 ,7 ,8 }; 14 15 //第五次结果 16 { 0 ,2 ,5 ,6 ,7 ,8 } 7 ==> { 0 ,2 ,5 ,6 ,7 ,8 };
如果存在N的数据需要排序的情况下,那么需要比较的次数第一次为N-1,第二次为N-2……那么,总次数为(N-1)*N/2即时间复杂度为O(n2)
下面是偷了维基上的一张图

| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最差时间复杂度 | О(n²) |
| 最优时间复杂度 | О(n²) |
| 平均时间复杂度 | О(n²) |
| 最差空间复杂度 | О(n) total, O(1) auxiliary |
算法实现:
C实现:
1 void sort(int src[] , int len ) 2 { 3 for( int n = 0 ; n < len ; n++) 4 { 5 int swapIndex = n; 6 for( int m = n+1 ; m < len ; m++) 7 { 8 if( src[ swapIndex ] > src[m] ) 9 { 10 swapIndex = m; 11 } 12 } 13 if( swapIndex != n) 14 { 15 int swap = src[n]; 16 src[n] = src[swapIndex]; 17 src[swapIndex] = swap; 18 } 19 } 20 }
C++实现:
1 template< typename T> 2 struct type_compare_bigger{ 3 int operator()( const T & left , const T& right){ 4 return left > right ; 5 } 6 }; 7 template< typename T> 8 struct type_compare_smaller{ 9 int operator()( const T & left , const T& right){ 10 return left > right ; 11 } 12 }; 13 template< typename T> 14 struct type_compare_equal{ 15 int operator()( const T & left , const T& right){ 16 return left == right; 17 } 18 }; 19 const double exp_float = 0.000001; 20 template< > 21 struct type_compare_bigger<float>{ 22 bool operator()( const float & left , const float& right){ 23 return (left - right) > exp_float ; 24 } 25 }; 26 template< > 27 struct type_compare_smaller<float>{ 28 bool operator()( const float & left , const float& right){ 29 return (left - right) < -exp_float ; 30 } 31 }; 32 template< > 33 struct type_compare_equal<float >{ 34 int operator()( const float & left , const float& right){ 35 return ((left - right) >= -exp_float) && ((left - right) <= exp_float); 36 } 37 }; 38 39 template< typename T > 40 struct swap{ 41 void operator()( T* left , T* right){ 42 T t = *left; 43 *left = *right; 44 *right = t; 45 } 46 }; 47 48 typedef unsigned int array_size; 49 template< typename T , typename C = type_compare_bigger<T> ,typename S= swap<T> > 50 struct algorithm{ 51 void operator()( T src[] , array_size len ){ 52 C comp ; 53 S swap; 54 for( array_size n = 0 ; n < len ; n++) 55 { 56 int swapIndex = n; 57 for( array_size m = n+1 ; m < len ; m++) 58 { 59 if(comp(src[swapIndex],src[m])){ 60 swapIndex = m; 61 } 62 } 63 if( swapIndex != n) 64 { 65 swap(&src[swapIndex],&src[n]); 66 } 67 } 68 69 } 70 }; 71 72 template< typename T > 73 void derect_select_sort( T src[] , array_size len) 74 { 75 algorithm<T> sort; 76 sort(src , len); 77 }
C++代码略显复杂了一些,有的人可能会认为是将简单问题复杂化了。其实我在写的时候我也在想有没有必要用模板特化来做,但想着想着还是这么实现了,我觉得,即使是将问题复杂化了,那么这里的代码也能给人一些启示。
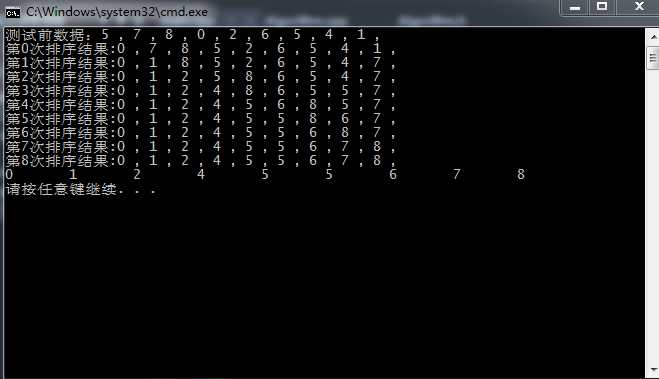
测试结果:
标签:
原文地址:http://www.cnblogs.com/jvane/p/4494640.html