标签:
很多玩过飞行射击类游戏的朋友都对跟踪导弹印象深刻,手中有这样一款武器常常能够战无不胜,但是敌人射出的导弹则可能成为玩家的噩梦。其实实现导弹跟踪的方法并不复杂,只需要一些简单的平面解析几何知识就可以做到。
算法分析 假设导弹旋转角速度为omega,运动速度为v。下图显示了导弹和目标在坐标轴中的初始状态。
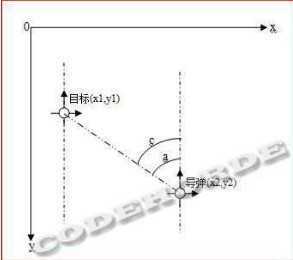
初始时刻,目标与导弹的运动方向都是-Y,位置分别为(x1,y1),(x2,y2),连接导弹与目标的坐标,得到一条线段,该线段与-Y轴夹角为c;导弹与-Y方向的夹角为b,b是导弹已旋转的角度,此时为0;导弹方向与线段的夹角为a,a就是导弹还需要旋转的角度。此时:
c=90-Math.atan2(y2-y1,x2-x1)*180/Math.PI; b=0; a=c-b;
为了方便计算将c转换为360度以内的正值:
c=(270+Math.atan2(y2-y1,x2-x1)*180/Math.PI)%360;
取得这些值以后,可以计算下一时刻导弹的旋转角度和应该处在的位置。如果a小于角速度omega,导弹旋转角度a,正好可以指向目标,否则将旋转omega度,所以 b=a<omega?a:omega; 复制代码导弹位置变更为
x2=x2+Math.sin(b*Math.PI/180)*v; y2=y2+Math.cos(b*Math.PI/180)*v;
在新的时刻,目标移动到新的位置,同时导弹旋转角度为b,如下图
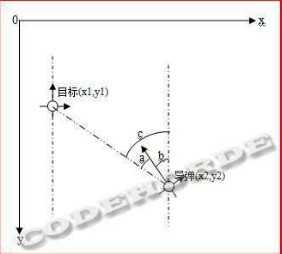
然后重新进行上面的计算,修正导弹位置和旋转角度,如此反复,直到导弹命中目标,或者因超出时间限制而销毁。
标签:
原文地址:http://www.cnblogs.com/lihonglin2016/p/4498689.html