标签:
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。
这些概念性的东西读起来总是很绕口,其实我们在处理堆排序的时候只需要知道以下几点就好了。
在用堆排序进行排序的时候我们先要构建堆,那么什么是堆呢?怎么构建呢?
在排序的时候每次将最后一个节点与堆的根节点交换,然后重组堆。
构建大顶堆的过程:
堆排序:
说明:堆排序的时间复杂度为O(nlog2n).跟快速排序一样,但是在实际排序中,快速排序总是比堆排序要快很多。
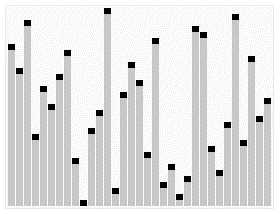
堆排序算法的演示。首先,将元素进行重排,以符合堆的条件。图中排序过程之前简单的绘出了堆树的结构。
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最差时间复杂度 |  |
| 最优时间复杂度 |  [1] [1] |
| 平均时间复杂度 |  |
| 最差空间复杂度 |  total, total,  auxiliary auxiliary |
C代码:
调整堆代码如下,如果用递归函数处理会容易理解很多,但是递归处理我认为在不需要的情况下最好不要,处理不好就是灾难性的,另外无限的分配栈,也会让资源吃紧。
1 void adjust_heap( int src[] , int len , int adjusting ) 2 { 3 for( int adj = adjusting ; adj < len ; ){ 4 int lchild = adj*2+1; 5 int rchild = adj*2+2; 6 if( lchild >= len ) break; 7 8 if( rchild >= len ) { 9 if( src[lchild] < src[adjusting] ){ 10 int temp = src[lchild]; 11 src[lchild] = src[adjusting]; 12 src[adjusting] = temp; 13 adj = lchild; 14 }else break; 15 }else{ 16 //adj = src[adj]<src[lchild] ? src[adj] < src[rchild] ? adj : rchild : src[lchild] < src[rchild] ? lchild : rchild; 17 int litter = src[lchild] < src[rchild] ? lchild : rchild; 18 litter = src[adj] < src[litter] ? adj : litter ; 19 if( litter == adj ){ 20 break; 21 }else{ 22 int temp = src[adj]; 23 src[adj] = src[litter]; 24 src[litter] = temp; 25 adj = litter; 26 } 27 } 28 } 29 }
堆排序算法代码:
1 void heap_sort( int src[] , int len) 2 { 3 for( int n = len/2 ; n >= 0 ; n-- ){ 4 adjust_heap(src,len,n); 5 } 6 7 for( int n = 0 ; n < len - 1 ; n++ ){ 8 int temp = src[0]; 9 src[0] = src[len -1 - n]; 10 src[len - 1 - n] = temp ; 11 adjust_heap(src,len-n-1,0); 12 } 13 }
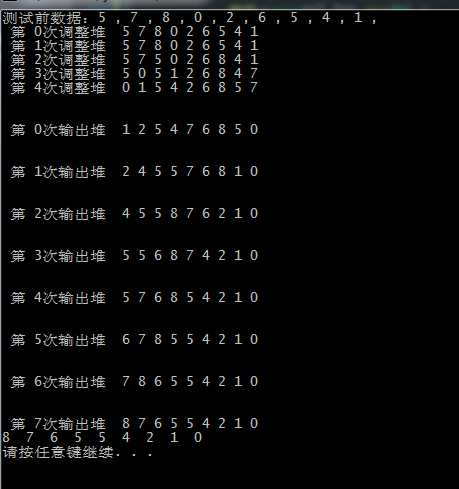
执行测试结果如下:
标签:
原文地址:http://www.cnblogs.com/jvane/p/4494641.html