标签:

对于上面那张图,是可以用dij算法求解出正确答案,但那只是巧合而已。
我们再看看下面这张图。
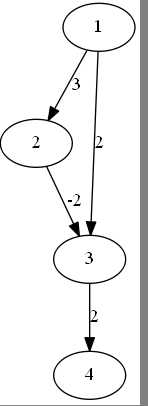
dist[4] 是不会被正确计算的。 因为dij算法认为从队列出来的点,(假设为u)肯定是已经求出最短路的点,标记点u。并用点u更新其它点。
所以如果存在负权使得这个点的权值更小,那么会更新dist[u], 但是因为这个点已经被标记了,所以dij算法不会用这个点来更新其它点,所以就导致了算法的错误。
归结原因,dij算法在存在负权的时候,过早得确立某个点最短路,以至于如果这个点不是最短路,就会导致错误。
如下面的算法所示

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 18 const int N = 1000 + 10; 19 struct Edge 20 { 21 int to,dist; 22 bool operator<(const Edge&rhs)const 23 { 24 return dist > rhs.dist; 25 } 26 }; 27 vector<Edge> g[N]; 28 int dist[N]; 29 bool vis[N]; 30 void dij(int start, int n) 31 { 32 memset(vis,0,sizeof(vis)); 33 for(int i=1; i<=n; ++i) 34 dist[i] = INF; 35 priority_queue<Edge> q; 36 Edge tmp,cur; 37 dist[start] = cur.dist = 0; 38 cur.to = start; 39 q.push(cur); 40 while(!q.empty()) 41 { 42 cur = q.top(); q.pop(); 43 int u = cur.to; 44 45 /* 46 如果u被用来更新过其它点,那么即使存在负权使得dist[u]变小, 47 那么dij算法也不会再用u来更新其它点,这就是dij不能处理负权回路的原因 48 */ 49 if(vis[u]) continue; 50 vis[u] = true; 51 for(int i=0; i<g[u].size(); ++i) 52 { 53 int v = g[u][i].to; 54 if(dist[v] > dist[u] + g[u][i].dist) 55 { 56 tmp.dist = dist[v] = dist[u] + g[u][i].dist; 57 tmp.to = v; 58 q.push(tmp); 59 } 60 } 61 } 62 63 } 64 65 int main() 66 { 67 int n,m,a,b,c,i; 68 Edge tmp; 69 while(scanf("%d%d",&n,&m)!=EOF) 70 { 71 for(i=0; i<m; ++i) 72 { 73 scanf("%d%d%d",&a,&b,&c); 74 tmp.to = b; 75 tmp.dist= c; 76 g[a].push_back(tmp); 77 } 78 dij(1,n); 79 for(i=1; i<=n; ++i) 80 printf("%d ",dist[i]); 81 puts(""); 82 } 83 return 0; 84 }
4 4
1 2 3
1 3 2
2 3 -2
3 4 2
dist[0->4] = 0 3 1 4; wrong
那么我们可以对上面的算法进行改进,上面算法的问题在于,一个点如果被标记以后,那么这个点是不会用来更新其它点的,哪怕到这个点的最短路径减小了,也不会用来更新其它点。
所以新的改进是我们允许一个点出队列多次,只要这个点对最短路的更新有贡献。
只要dist[u]>=cur.dist , 那么我们就认为点u可能对最短路的更新有贡献,所以让点u去更新最短路。

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 3 3 19 1 2 3 20 1 3 2 21 2 3 -2 22 23 24 4 4 25 1 2 3 26 1 3 2 27 2 3 -2 28 3 4 2 29 dist[0->4] = 0 3 1 3; correct 30 31 */ 32 const int N = 1000 + 10; 33 struct Edge 34 { 35 int to,dist; 36 bool operator<(const Edge&rhs)const 37 { 38 return dist > rhs.dist; 39 } 40 }; 41 vector<Edge> g[N]; 42 int dist[N]; 43 //允许一个点入队列多次,是spfa算法, 可以看做是dij的变种或者bellman的变种 44 void spfa(int start, int n) 45 { 46 for(int i=1; i<=n; ++i) 47 dist[i] = INF; 48 priority_queue<Edge> q; 49 Edge tmp,cur; 50 dist[start] = cur.dist = 0; 51 cur.to = start; 52 q.push(cur); 53 while(!q.empty()) 54 { 55 cur = q.top(); q.pop(); 56 int u = cur.to; 57 if(dist[u]<cur.dist) continue; //这里就是允许点u用来多次更新其它点的关键 58 for(int i=0; i<g[u].size(); ++i) 59 { 60 int v = g[u][i].to; 61 if(dist[v] > dist[u] + g[u][i].dist) 62 { 63 tmp.dist = dist[v] = dist[u] + g[u][i].dist; 64 tmp.to = v; 65 q.push(tmp); 66 } 67 } 68 } 69 70 } 71 72 int main() 73 { 74 int n,m,a,b,c,i; 75 Edge tmp; 76 while(scanf("%d%d",&n,&m)!=EOF) 77 { 78 for(i=0; i<m; ++i) 79 { 80 scanf("%d%d%d",&a,&b,&c); 81 tmp.to = b; 82 tmp.dist= c; 83 g[a].push_back(tmp); 84 } 85 dij(1,n); 86 for(i=1; i<=n; ++i) 87 printf("%d ",dist[i]); 88 puts(""); 89 } 90 return 0; 91 }
4 4
1 2 3
1 3 2
2 3 -2
3 4 2
dist[0->4] = 0 3 1 3; correct
标签:
原文地址:http://www.cnblogs.com/justPassBy/p/4511418.html