标签:
在有根树中,两个结点u和v的公共祖先中距离最近的那个称为最近公共祖先(lowest common ancestor)、
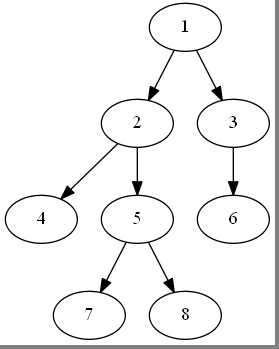
如图lca(4,7) = 2, lca(6,8)=1, lca(5,8)=5
记点v到根的深度为depth[v], 那么如果w是点u和v的公共祖先的话, 让u向上走depth[u] - depth[w]步,让v向上走depth[v]-depth[w]步,都将走到w
因此让u和v中较深的一个向上走|depth[u]-depth[v]|步,然后再一步步向上走,直到走到同一个结点,就可以再O(n)的时间内求出LCA

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 8 7 19 1 2 20 1 3 21 2 4 22 2 5 23 5 7 24 5 8 25 3 6 26 */ 27 const int N = 1000 + 10; 28 vector<int> g[N]; 29 int parent[N],depth[N]; 30 void dfs(int u, int p, int d)//求出每个点的depth和parent 31 { 32 parent[u] = p; 33 depth[u] = d; 34 for(int i=0; i<g[u].size(); ++i) 35 { 36 if(g[u][i]!=p) 37 dfs(g[u][i],u,d+1); 38 } 39 } 40 void init() 41 { 42 dfs(1,-1,0); 43 } 44 int lca(int u, int v) 45 { 46 //让u和v向上走到同一深度 47 while(depth[u] > depth[v]) u = parent[u] ; 48 while(depth[v] > depth[u]) v = parent[v] ; 49 //让u和v走到同一结点 50 while(u!=v) 51 { 52 u = parent[u]; 53 v = parent[v]; 54 } 55 return u; 56 } 57 int main() 58 { 59 int n,m,i,a,b; 60 while(scanf("%d%d",&n,&m)!=EOF) 61 { 62 for(i=0; i<m; ++i) 63 { 64 scanf("%d%d",&a,&b); 65 g[a].push_back(b); 66 g[b].push_back(a); 67 } 68 init(); 69 while(scanf("%d%d",&a,&b)!=EOF) 70 { 71 printf("%d\n",lca(a,b)); 72 } 73 } 74 return 0; 75 }
我们可以用二分搜索来求出走到公共祖先所需要的最少步数
只要预处理出parent数组
parent2[v] = parent[parent[v]], parent4 = parent2[parent2[v]] 以此类推,我们就能得到向上走2^k步所能达到的顶点parent[k][v]
预处理parent[k][v]的时间复杂度为O(nlogn)

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 const int MAX_LOG_V = 100; 21 const int MAX_V = 1000+10; 22 int parent[MAX_LOG_V][MAX_V]; 23 int depth[MAX_V]; 24 vector<int> g[MAX_V]; 25 int cnt[MAX_V]; 26 void dfs(int u, int fa, int d) 27 { 28 parent[0][u] = fa; 29 depth[u] = d; 30 for(int i=0; i<g[u].size(); ++i) 31 if(g[u][i]!=fa) 32 dfs(g[u][i],u,d+1); 33 } 34 void init(int root, int n) 35 { 36 dfs(root,-1,0); 37 //预处理出parent 38 for(int k=0; k+1<MAX_LOG_V; ++k) 39 { 40 for(int v=1; v<=n; ++v) 41 { 42 if(parent[k][v]<0) 43 parent[k+1][v] = -1; 44 else 45 parent[k+1][v] = parent[k][parent[k][v]]; 46 } 47 } 48 } 49 void swap(int &a, int &b) 50 { 51 int t = a; 52 a = b; 53 b = t; 54 } 55 int lca(int u, int v) 56 { 57 if(depth[u] < depth[v]) 58 swap(u,v); 59 //让u和v走到同一生度 60 for(int k=0; k<MAX_LOG_V; ++k) 61 if((depth[u]-depth[v])>>k&1)//一个数能分解成多个二进制数相加,所以如果&1 为true,那么就向上走 62 u = parent[k][u]; 63 if(u==v) return u; 64 //达到同一深度后,二分搜索lca 65 66 for(int k=MAX_LOG_V-1; k>=0; --k) 67 if(parent[k][v]!=parent[k][u]) 68 {//我们并不知道要向上走多少步,但是只要每次走后, 69 //parent[k][v]!=parent[k][u],那么这一步就可以向上走,即将要走的步数分解为 1 + 2 + 4 + 8 + ...最后一步将在循环结束后走出 70 u = parent[k][u]; 71 v = parent[k][v]; 72 } 73 return parent[0][u]; 74 } 75 void input(int &x) 76 { 77 char ch = getchar(); 78 while(ch>‘9‘ || ch<‘0‘) 79 ch = getchar(); 80 x = 0; 81 while(ch>=‘0‘ && ch<=‘9‘) 82 { 83 x = x * 10 + ch - ‘0‘; 84 ch = getchar(); 85 } 86 } 87 int main() 88 { 89 int n,a,m,i,b; 90 while(scanf("%d%d",&n,&m)!=EOF) 91 { 92 for(i=0; i<m; ++i) 93 { 94 scanf("%d%d",&a,&b); 95 g[a].push_back(b); 96 g[b].push_back(a); 97 } 98 init(1,n); 99 while(scanf("%d%d",&a,&b)!=EOF) 100 { 101 printf("%d\n",lca(a,b)); 102 } 103 } 104 105 return 0; 106 }
用上面的模板求lca就可以了,然后记录下来。 输入很恶心, 但是学到了用input读输入

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 const int MAX_LOG_V = 100; 21 const int MAX_V = 1000+10; 22 int parent[MAX_LOG_V][MAX_V]; 23 int depth[MAX_V]; 24 vector<int> g[MAX_V]; 25 int cnt[MAX_V]; 26 void dfs(int u, int fa, int d) 27 { 28 parent[0][u] = fa; 29 depth[u] = d; 30 for(int i=0; i<g[u].size(); ++i) 31 if(g[u][i]!=fa) 32 dfs(g[u][i],u,d+1); 33 } 34 void init(int root, int n) 35 { 36 dfs(root,-1,0); 37 for(int k=0; k+1<MAX_LOG_V; ++k) 38 { 39 for(int v=1; v<=n; ++v) 40 { 41 if(parent[k][v]<0) 42 parent[k+1][v] = -1; 43 else 44 parent[k+1][v] = parent[k][parent[k][v]]; 45 } 46 } 47 } 48 void swap(int &a, int &b) 49 { 50 int t = a; 51 a = b; 52 b = t; 53 } 54 int lca(int u, int v) 55 { 56 if(depth[u] < depth[v]) 57 swap(u,v); 58 for(int k=0; k<MAX_LOG_V; ++k) 59 if((depth[u]-depth[v])>>k&1) 60 u = parent[k][u]; 61 if(u==v) return u; 62 for(int k=MAX_LOG_V-1; k>=0; --k) 63 if(parent[k][v]!=parent[k][u]) 64 { 65 u = parent[k][u]; 66 v = parent[k][v]; 67 } 68 return parent[0][u]; 69 } 70 void input(int &x) 71 { 72 char ch = getchar(); 73 while(ch>‘9‘ || ch<‘0‘) 74 ch = getchar(); 75 x = 0; 76 while(ch>=‘0‘ && ch<=‘9‘) 77 { 78 x = x * 10 + ch - ‘0‘; 79 ch = getchar(); 80 } 81 } 82 int main() 83 { 84 int n,a,m,i,b; 85 char str[11]; 86 char ch; 87 int root; 88 while(scanf("%d",&n)!=EOF) 89 { 90 for(i=1; i<=n; ++i) 91 { 92 g[i].clear(); 93 parent[0][i] = -1; 94 } 95 for(i=1; i<=n; ++i) 96 { 97 input(a); 98 input(m); 99 for(int j=0; j<m; ++j) 100 { 101 input(b); 102 g[a].push_back(b); 103 parent[0][b] = a; 104 } 105 } 106 root = n; 107 while(parent[0][root]!=-1) 108 root = parent[0][root]; 109 for(i=1; i<=n; ++i) 110 { 111 parent[0][i] = 0; 112 cnt[i] = 0; 113 } 114 init(root,n); 115 input(m); 116 for(i=0; i<m; ++i) 117 { 118 input(a); 119 input(b); 120 a = lca(a,b); 121 cnt[a]++; 122 } 123 for(i=1; i<=n; ++i) 124 if(cnt[i]!=0) 125 printf("%d:%d\n",i,cnt[i]); 126 } 127 return 0; 128 }
标签:
原文地址:http://www.cnblogs.com/justPassBy/p/4513217.html