标签:
博文“二分图的最大匹配、完美匹配和匈牙利算法”对二分图相关的几个概念讲的特别形象,特别容易理解。本文介绍部分主要摘自此博文。
还有其他可参考博文:
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集 U 和V ,使得每一条边都分别连接U、V中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。




我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法,下面讲的概念都为这个算法服务。

交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):

增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前,先讲一下匈牙利树。
匈牙利树一般由 BFS 构造(类似于 BFS 树)。从一个未匹配点出发运行 BFS(唯一的限制是,必须走交替路),直到不能再扩展为止。例如,由图 7,可以得到如图 8 的一棵 BFS 树:



这棵树存在一个叶子节点为非匹配点(7 号),但是匈牙利树要求所有叶子节点均为匹配点,因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点,那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示(顺便说一句,图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配)。
匈牙利算法可基于DFS或BFS实现。本文实现的是基于DFS的。
具体代码头文件定义为:
1 #ifndef HUNGARIAN_H 2 #define HUNGARIAN_H 3 4 #include "BFS_n_DFS.h" // 详细代码请转到Github. 5 6 class Graph_Hun : public Graph_BD 7 { 8 public: 9 Graph_Hun(); 10 virtual ~Graph_Hun(); 11 virtual bool DFS(int vexID); 12 virtual bool BFS(int vexID); 13 int hungarian(); 14 15 void setNumOfLeft(int num); 16 void setNumOfRight(int num); 17 18 private: 19 int matching[MAXNUM]; 20 bool checked[MAXNUM]; 21 int numOfLeft; 22 int numOfRight; 23 }; 24 25 #endif
实现文件为:

1 #include "Hungarian.h" 2 #include <cassert> 3 4 Graph_Hun::Graph_Hun() 5 { 6 memset(matching, -1, sizeof(matching)); 7 memset(checked, false, sizeof(checked)); 8 } 9 10 Graph_Hun::~Graph_Hun() 11 { 12 13 } 14 15 bool Graph_Hun::DFS(int vexID) 16 { 17 assert(vexID >= 0 && vexID < MAXNUM); 18 19 vector<int> adjVexes = adj(vexID); 20 int sz = adjVexes.size(); 21 for (int i = 0; i < sz; i++) 22 { 23 int adjVex = adjVexes[i]; 24 if (!checked[adjVex]) 25 { 26 checked[adjVex] = true; 27 if (matching[adjVex] == -1 || DFS(matching[adjVex])) 28 { 29 matching[adjVex] = vexID; 30 matching[vexID] = adjVex; 31 return true; 32 } 33 } 34 } 35 return false; 36 } 37 38 bool Graph_Hun::BFS(int vexID) 39 { 40 return true; 41 } 42 43 int Graph_Hun::hungarian() 44 { 45 int maxMatching = 0; 46 for (int i = 0; i < numOfLeft; i++) 47 { 48 if (matching[i] == -1) 49 { 50 memset(checked, false, sizeof(checked)); 51 if (DFS(i)) 52 maxMatching++; 53 } 54 } 55 return maxMatching; 56 } 57 58 void Graph_Hun::setNumOfLeft(int num) 59 { 60 numOfLeft = num; 61 } 62 63 void Graph_Hun::setNumOfRight(int num) 64 { 65 numOfRight = num; 66 }
下边将用一个例子来说明利用匈牙利算法求二分图最大匹配的过程。作为例子的二分图如下:
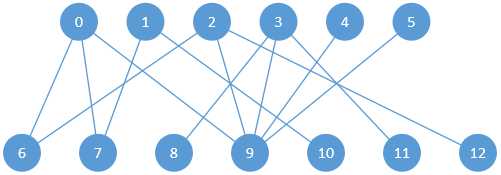
图2-1 一个二分图(其中0~1表示二分图左边,6~12表示二分图右边)
详细的二分图最大匹配过程如下图所示:
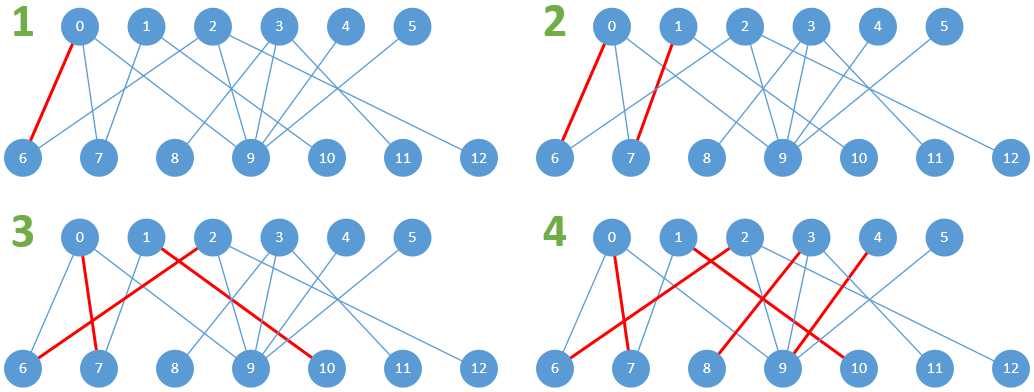
图2-2 详细的二分图最大匹配过程
在子图1中,0直接连接到6;在子图2中,1直接连接到7;在子图3中,2试图连接到6(因为是DFS搜索),但6已经连接到0,这时候就要找增广路径了,找到的路径如下图:
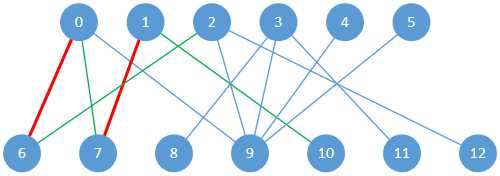
图2-3 增广路径“2->6->0->7->1->10”
这时将已匹配和未匹配的路径反转就能够得到图2-2中的子图3了。在图2-2的子图4中,3、4分别直接连接到8、9,没有寻找增广路径的过程。而对5来说,并未能找到增广路径,因此5无法匹配。最终的匹配结果如下图:
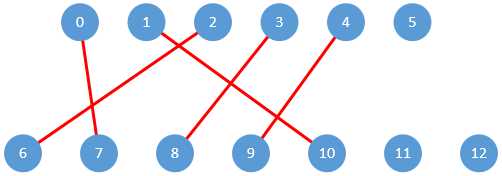
图2-4 二分图最终匹配结果
详细代码请参考自Github.
"《算法导论》之‘图’":不带权二分图最大匹配(匈牙利算法)
标签:
原文地址:http://www.cnblogs.com/xiehongfeng100/p/4518386.html