标签:
核心思想:以起始原点为中心,想外层扩展,知道扩展到重点为止。
设到A点的最短路径上,A点前驱节点为B,则该路径包含到达节点B的最短路径。
S集合代表已经探索过的节点,U集合表示未探索过的节点。
时间复杂度为O(n^2)
具体过程见下图和表
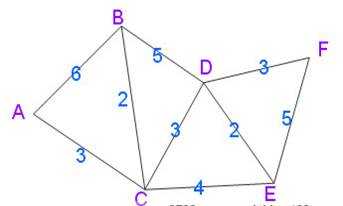

C++代码如下:

1 #include<stdio.h> 2 #define MAXDIS 4294967295 3 using namespace std; 4 5 class MatrixGraphic{ 6 public: 7 MatrxiGraphic(int number=0){ 8 this->vertexNum = number; 9 vertex = new int[vertexNum]; 10 arc = new int *[vertexNum]; 11 for(int i=0;i<vertexNum;i++) 12 { 13 arc[i]=new int[vertex]; 14 for(int j=0;j<vertexNum;j++) 15 { 16 arc[i][j] = MAXDIS; 17 } 18 } 19 } 20 21 int getValueOfEdge(int start,int end) 22 { 23 return arc[start][end];j 24 } 25 int getVertexNumber() 26 { 27 return vertexNum; 28 } 29 30 void setValueOfEdge(int start,int end,int value) 31 { 32 this->arc[start][end] = value; 33 } 34 private: 35 int vertexNum; 36 int *vertex; 37 int **arc; 38 } 39 40 void dijkstra(MatrixGraphic *graphic,int s,int *dist,int *prev) 41 { 42 int vertexNUm = graphic->getVertexNumber(); 43 bool *S = new bool[vertexNum]; 44 for(int i=0;i<vertexNum;i++) 45 { 46 dist[i]=graphic->getValueOfEdge(s,i); 47 S[i]=false; 48 if(dist[i]==MAXDIS) 49 { 50 prev[i]=-1; 51 } 52 else 53 { 54 prev[i]=s; 55 } 56 } 57 58 dist[s]=0; 59 S[s] = true; 60 61 for(int i=1;i<vertexNum;i++) 62 { 63 int temp = MAXDIS; 64 int u=s; 65 for(int j=0;j<vertexNum;j++) 66 { 67 if(!S[j] && dist[j]<temp) 68 { 69 u=j; 70 temp = dist[j]; 71 } 72 } 73 S[u]=true; 74 for(int j=0;j<vertexNum;j++) 75 { 76 int edge = graphic->getValueOfEdge(u,j); 77 if(!S[i] && edge<MAXDIS) 78 { 79 int newDist = dist[u]+edge; 80 if(newDist<dist[j]) 81 { 82 dist[j]=newDist; 83 prev[j]=u; 84 } 85 } 86 } 87 } 88 89 for(int i=0;i<vertexNum;i++) 90 { 91 int *stack = new int[vertexNum]; 92 int top = 0; 93 stack[top]=i; 94 top++; 95 int tempVertex = prev[i]; 96 while(tempVertex != s) 97 { 98 stack[top]=tempVertex; 99 top++; 100 tempVertex = prev[tempVertex]; 101 } 102 stack[top] = s; 103 for(int j=top;j>=0;j--) 104 { 105 if(j!=0) 106 { 107 cout<<stack[top]<<"->"; 108 } 109 else 110 { 111 cout<<stack[top]<<endl; 112 } 113 } 114 } 115 }
标签:
原文地址:http://www.cnblogs.com/yueyanglou/p/4518534.html