标签:
一.求解步骤
1.矩阵必须是方阵(即矩阵的行列相等)。
2.矩阵可逆的充分必要条件是其行列式的值不为零。
3.求出矩阵的伴随矩阵。
4.逆矩阵=行列式值的倒数*伴随矩阵。
二.算法
#include <stdio.h> #include <stdlib.h> void main() { int i,j; int dimension; double deterValue=1; double **array,**deterArray, **companionMatrix, *temp; //声明函数 void printfDouble2Dimension(int s, int n, double **array); double deter(int dimension, double **array); void copyDouble2Dimension(int s, int n, double **source, double **dest); void getCompanionMatrix(int dimension, double **array, double **companionMatrix); printf("请输入方阵的阶数N:"); scanf("%d",&dimension); array=(double**)malloc(dimension*sizeof(double*)); deterArray=(double**)malloc(dimension*sizeof(double*)); companionMatrix =(double**)malloc(dimension*sizeof(double*)); //循环输入方阵 for(i=0;i<dimension;i++) { temp=(double*)malloc(dimension*sizeof(double)); deterArray[i]=(double*)malloc(dimension*sizeof(double)); companionMatrix[i]=(double*)malloc(dimension*sizeof(double)); printf("请输入方阵的第%d行:",i+1); for(j=0;j<dimension;j++) scanf("%lf",temp+j); array[i]=temp; } //拷贝数组 copyDouble2Dimension(dimension,dimension,array,deterArray); //打印方阵 printf("方阵初等变换之前如下:\n"); printfDouble2Dimension(dimension,dimension,array); deterValue = deter(dimension,deterArray); printf("方阵初等变换之后如下:\n"); printfDouble2Dimension(dimension,dimension,deterArray); if(deterValue==0) { printf("方阵行列式值为零.\n"); system("pause"); return ; } printf("行列式的值:%.2lf\n",deterValue); //求伴随矩阵 getCompanionMatrix(dimension,array,companionMatrix); //打印伴随矩阵 printf("伴随矩阵如下:\n"); printfDouble2Dimension(dimension, dimension, companionMatrix); system("pause"); } //求伴随矩阵 void getCompanionMatrix(int dimension, double **array, double **companionMatrix) { int i,j,k,l,m,n,o; int flag;//标志代数余子式的符号 double **companionTemp; double deter(int dimension,double **array); companionTemp =(double**)malloc((dimension-1)*sizeof(double*)); for(i=0;i<dimension-1;i++) companionTemp[i]=(double*)malloc((dimension-1)*sizeof(double)); for(i=0;i<dimension;i++) { for(j=0;j<dimension;j++) { flag=(i+j)%2==0?1:-1; for(k=0,m=0;k<dimension;k++) { if(k==i)continue; for(l=0,n=0;l<dimension;l++) { if(l==j)continue; *(*(companionTemp+m)+n) = *(*(array+k)+l); n++; } m++; } //第i行,第j列的代数余子式 赋值给第j行,第i列 *(*(companionMatrix+j)+i) = flag * deter(dimension-1,companionTemp); } } } /* * calculate the determinant value */ double deter(int dimension,double **array) { int i,j,k,l,b; int flag =1; double sum=1; double temp; for(i=0,j;i<dimension-1;i++) { j=i; if(*(*(array+i)+j)==0) { b=0; for(k=i+1;k<dimension;k++) { if(*(*(array+k)+j)!=0)//找到一行不为0的,然后换行 { for(l=j;l<dimension;l++) { temp=*(*(array+k)+l); *(*(array+k)+l)= *(*(array+i)+l); *(*(array+i)+l)=temp; } flag*=-1; b=1; break; } } if(!b) { return 0; } i--; continue; } for(;j<dimension-1;j++) { if(*(*(array+j+1)+i)==0) continue; temp = -*(*(array+j+1)+i)/ *(*(array+i)+i); for(k=i;k<dimension;k++) *(*(array+j+1)+k)+= *(*(array+i)+k)*temp; } } for(i=0;i<dimension;i++) sum*= *(*(array+i)+i); return sum*flag; } //打印数组 void printfDouble2Dimension(int s, int n, double **array) { //printf("%d,%d",s,n); int i,j; for(i=0;i<s;i++) { for(j=0;j<n;j++) { printf("%6.2lf",*(*(array+i)+j)); } printf("\n"); } } //拷贝数组 void copyDouble2Dimension(int s, int n, double **source, double **dest) { int i,j; for(i=0;i<s;i++) { for(j=0;j<n;j++) { *(*(dest+i)+j)=*(*(source+i)+j); } } }
三.程序截图
1> 习题3.3-2(2)
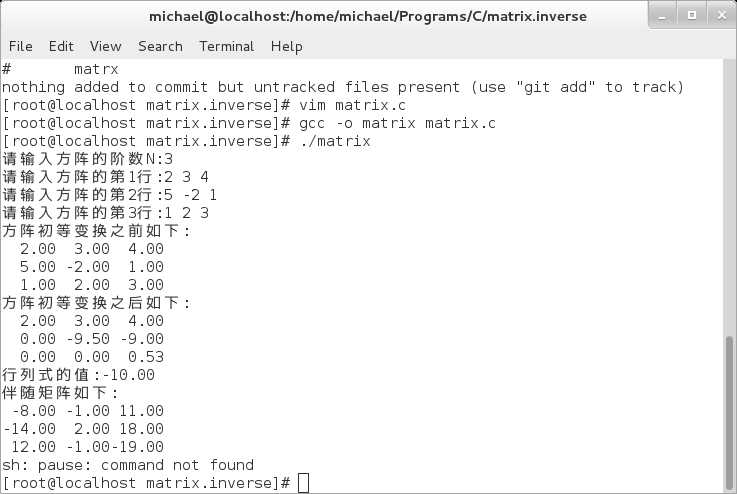
2> 习题3.3-2(3)
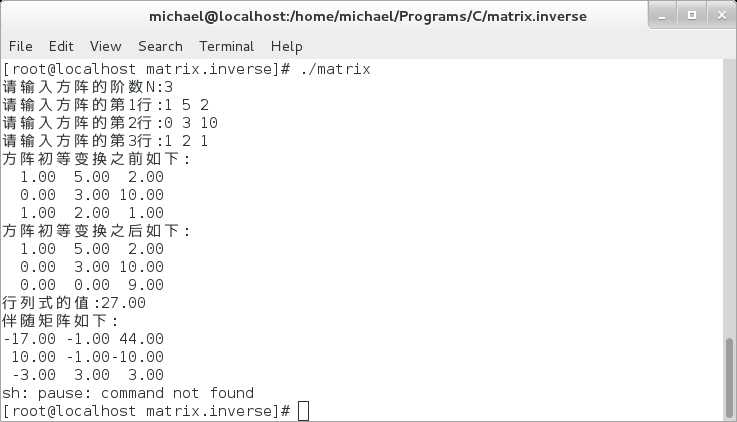
3> 习题3.3-2(4)
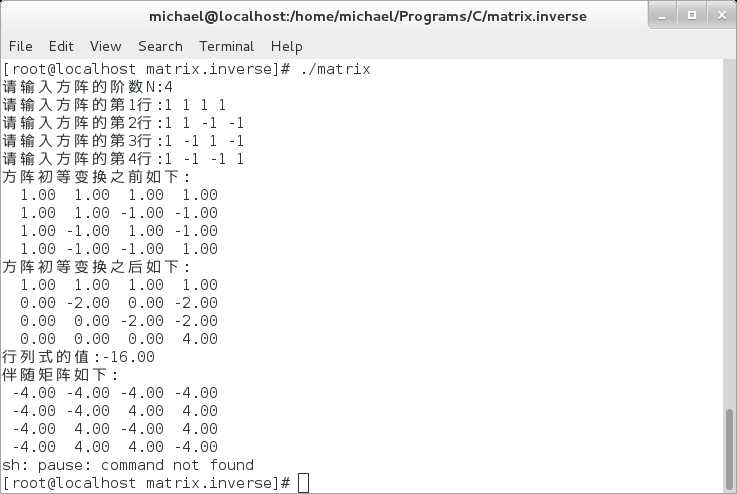
4> 习题3.3-2(5)
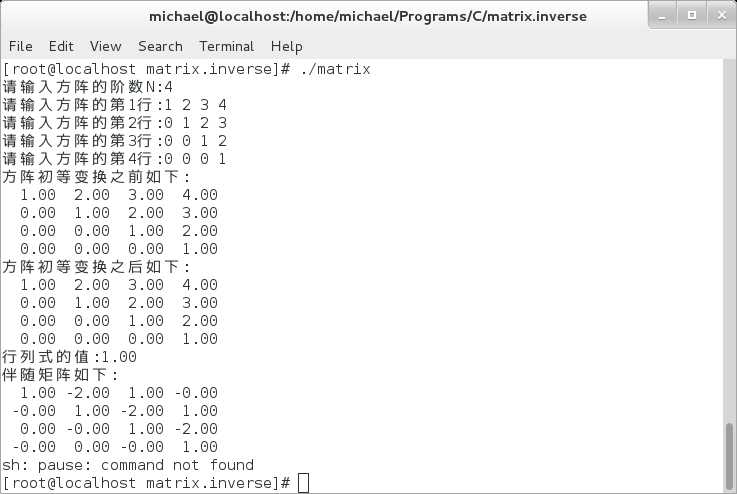
5> 习题3.3-7(2).1
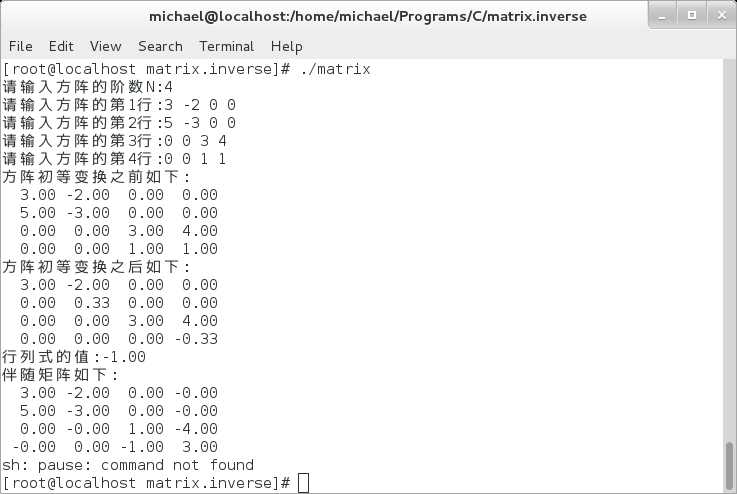
6> 习题3.3-7(2).2
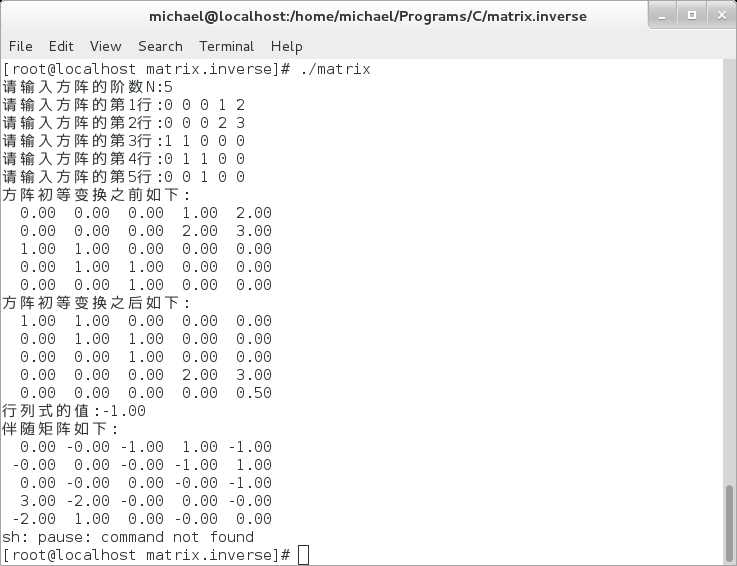
标签:
原文地址:http://www.cnblogs.com/tianzhenyun/p/4527742.html