标签:
1、代码
2、运行结果
3、分析
1、代码
#include <stdio.h> #include <stdlib.h> typedef struct _Node { int value; struct _Node * pLeft; struct _Node * pRight; } Node; Node * getNewNode(int iValue) { Node * p = (Node *)malloc(sizeof(Node)); if(NULL != p) { p->value = iValue; } return p; } void deleteNode(Node * p) { if(NULL != p) { free(p); } } int addElm(Node * p, int value) { Node * pX = p; while(pX) { if(value < pX->value) { if(NULL == pX->pLeft) { pX->pLeft = getNewNode(value); printf("add [%2d] to left of [%2d]\n", value, pX->value); break; } else { pX = pX->pLeft; } } else { if(NULL == pX->pRight) { pX->pRight = getNewNode(value); printf("add [%2d] to right of [%2d]\n", value, pX->value); break; } else { pX = pX->pRight; } } } return 0; } Node * makeBinaryTree(int iList[], int iNum) { Node * p = getNewNode(iList[0]); int i = 0; for(i = 1; i < iNum; i++) { addElm(p, iList[i]); } printf("\n"); return p; } void destroyBinaryTree(Node * p) { if(NULL == p) { return; } destroyBinaryTree(p->pLeft); destroyBinaryTree(p->pRight); free(p); } int preorderTraversal(Node * p) { if(NULL == p) { return -1; } printf("%2d ", p->value); preorderTraversal(p->pLeft); preorderTraversal(p->pRight); return 0; } int postorderTraversal(Node * p) { if(NULL == p) { return -1; } postorderTraversal(p->pLeft); postorderTraversal(p->pRight); printf("%2d ", p->value); return 0; } int inorderTraversal(Node * p) { if(NULL == p) { return -1; } inorderTraversal(p->pLeft); printf("%2d ", p->value); inorderTraversal(p->pRight); return 0; } void preTrvl(Node * p) { printf("pre : "); preorderTraversal(p); printf("\n"); } void postTrvl(Node * p) { printf("post : "); postorderTraversal(p); printf("\n"); } void inTrvl(Node * p) { printf("in : "); inorderTraversal(p); printf("\n"); } void printList(int iList[], int iNum) { for(int i = 0; i < iNum; i++) { printf("%d ", iList[i]); } printf("\n"); } int main() { int iList[15] = {8, 0, 3, 12, 11, 4, 13, 6, 10, 9, 1, 5, 14, 2, 7}; int iNum = 15; printList(iList, iNum); Node * p = makeBinaryTree(iList, iNum); preTrvl(p); postTrvl(p); inTrvl(p); destroyBinaryTree(p); }
2、运行结果
1 $ ./binaryTree 2 8 0 3 12 11 4 13 6 10 9 1 5 14 2 7 3 add [ 0] to left of [ 8] 4 add [ 3] to right of [ 0] 5 add [12] to right of [ 8] 6 add [11] to left of [12] 7 add [ 4] to right of [ 3] 8 add [13] to right of [12] 9 add [ 6] to right of [ 4] 10 add [10] to left of [11] 11 add [ 9] to left of [10] 12 add [ 1] to left of [ 3] 13 add [ 5] to left of [ 6] 14 add [14] to right of [13] 15 add [ 2] to right of [ 1] 16 add [ 7] to right of [ 6] 17 18 pre : 8 0 3 1 2 4 6 5 7 12 11 10 9 13 14 19 post : 2 1 5 7 6 4 3 0 9 10 11 14 13 12 8 20 in : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
3、分析
从运行结果的第三行开始,就是开始进行数据插入的地方,下面对运行结果中,每一行插入动作后二叉树的情况进行画图描述。
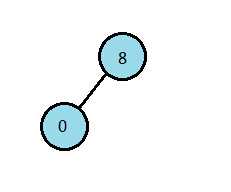
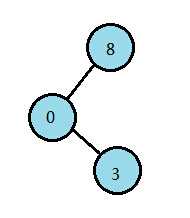
第03行 :add [ 0] to left of [ 8] 第04行: [ 3] to right of [ 0]
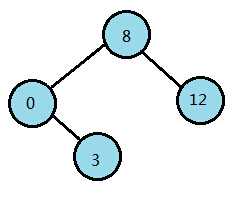
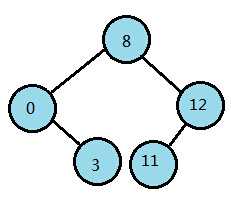
第05行:add [12] to right of [ 8] 第06行:add [11] to left of [12]
第07行:add [ 4] to right of [ 3] 第08行:add [13] to right of [12]
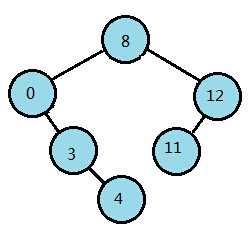
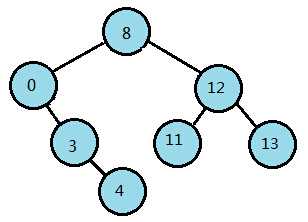
标签:
原文地址:http://www.cnblogs.com/fengbohello/p/4530968.html