Hungarian method （匈牙利算法）----解决指派问题（转）

　　

　　步骤一：将这系数矩阵进行变换，使各行各列都出现0元素．从系数矩阵的每行元素减去该行的最小元素即得每行每列都有有0元素的系数矩阵．

　　-------------------------------- 

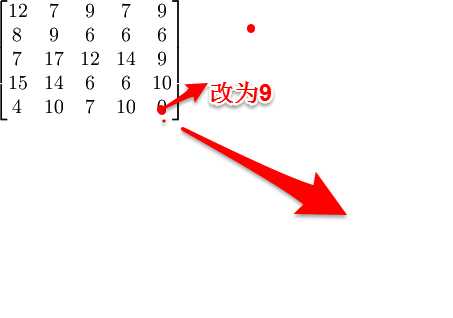　　步骤二：进行试指派，找出独立的0元素．独立0元素用Θ表示，其它0用Φ表示得到

　　……(1)

　　这里Θ的个数m=4,而n=5；问题没有得到求解，运用步骤三继续求解．

　　步骤三：作最少的直线覆盖所有的0元素，以确定该系数矩阵中能找到最多的独立元素数．为此按以下步骤进行．

　　(1)对没有Θ的行打√号：；

　　(2)对已打√号的行中所含0元素的列打√号；

　　(3)再对所有打√号的列中的含有@元素的行打√号；

　　(4)重复2、3直到得不出新的打√号的行列为止．

　　(5)对没有打√号的行画一横线，有打√号的列画一纵线，这就得到覆盖所有0元素的最少直线数．

　　令直线数为l．若l < n，说明必须再变换当前的系数矩阵，才能找到n个独立的0元素，为此转换步骤四；若l = n，而m < n，应回到步骤二，另行试探．

　　在此例中，对矩阵(1)按以下次序进行：

　　先在第五行旁打√，接着可判断应在第一列下打√，接着在第3行旁打√，经检查不能再打√了．对没有打√行画一直线以覆盖0元素，对打√的列画一直线以覆盖0元素，得：

　　……(2)

　　由此可见l = 4 < n．所以应继续对(2)矩阵进行变换转步骤四．

　　步骤四：对(2)矩阵进行变换的目的是增加0元素．

　　为此在没有被直线覆盖的部分中找出最小元素．然后在打√行各元素中都减去这个最小元素，而在打√列的各元素上都加上这个最小元素，以保证原来0元素不变．这样得到新系数矩阵(它的最优解和原问题相同)．若得到n个独立的0元素，则已得最优解，否则回到步骤三重复进行．

　　在矩阵(2)中，在没有被覆盖部分(第3、5行)中找到最小元素为2，然后在第3、5行各元素分别减去2。给第l列各元素加2，得到新矩阵(3)

　　……(3)

　　按步骤二，找出所有的独立0元素。得到矩阵(4)

　　……(4)

　　它具有n个独立0元素．这就得到了最优解，相应解矩阵为

　　由解矩阵得最优指派方案：

　　甲——B，乙——D，丙——E，丁——C，戊——A

　　所需总时间为minz=32．