【数学建模】【APIO2015】Palembang Bridges

一条东西走向的穆西河将巴邻旁市一分为二，分割成了区域 A 和区域 B。

每一块区域沿着河岸都建了恰好 1000000001 栋的建筑，每条岸边的建筑都从 0 编号到 1000000000。相邻的每对建筑相隔 1 个单位距离，河的宽度也是 1 个单位长度。区域 A 中的 i 号建筑物恰好与区域 B 中的 i 号建筑物隔河相对。

城市中有 N 个居民。第 i 个居民的房子在区域 Pi 的 Si 号建筑上，同时他的办公室坐落在 Qi 区域的 Ti 号建筑上。一个居民的房子和办公室可能分布在河的两岸，这样他就必须要搭乘船只才能从家中去往办公室，这种情况让很多人都觉得不方便。为了使居民们可以开车去工作，政府决定建造不超过 K 座横跨河流的大桥。

由于技术上的原因，每一座桥必须刚好连接河的两岸，桥梁必须严格垂直于河流，并且桥与桥之间不能相交。当政府建造最多 K 座桥之后，设 Di 表示第 i 个居民此时开车从家里到办公室的最短距离。请帮助政府建造桥梁，使得 D1+D2+?+DN 最小。

K=1或K=2

1≤N≤100000

题解

/*自己搞出来的一道题，真是好感动*/

为了方便，在同一侧的直接处理掉。

K=1时，显然就是取中位数。

K=2时，考虑每一对(S,T)，(绿蓝代表两座桥)，那么肯定是要选两条红线短的那一边。不过这样还不够好考虑，我们不如让着两条直线伸长相等的距离，延伸到中点。

技术分享

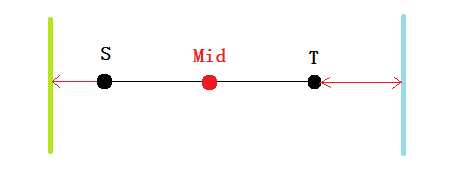
于是对于每一对(S,T)，直接看Mid到两墙的距离就可以选择了。

进一步得出，如果我们把它们按中点排序，那么最后的局面肯定是，左部分都去桥1，右部分都去桥2，有一个分割点。

那么我们可以枚举分割点，分别计算两部分的最优桥，很神奇的把K=2分成了两个K=1，得到n^2的算法。

显然最优桥我们是可以动态维护的。

考虑点i(一对ST)，把它从右部分加入左部分。

那么它对于最优桥的影响是可以讨论的，过程很傻逼可以自己试一试。

我得到的结果是，考虑左右部分肯定都是偶数，那么另左部分中位数取(len/2)，右部分中位数取(len/2+1)，这么做比较方便。

然后加点到左部分的时候，因为我们已经按中点排序，所以只可能是一左一右或者两右(左右是相对当前最优桥而言的)。

那么如果是一左一右，最优桥不发生变化，对ans新的贡献也就是这个点的贡献。

如果是两右，会使最优桥右移一位，但对于之前已加入的点是没有影响的，ans的改变还是只有这个点。

于是用两个树状数组模拟两边，每次求最优桥(这个也用树状数组求第k小数)，然后维护ans也就是计算当前点的影响就行了。

复杂度O(nlogn)。说不清还是看代码吧。

主要考察数学建模、对数据结构的应用，感觉这题还是蛮好的。

代码

代码能力各种逗啊QwQ 调了好久但调出来后真是好久没觉得这么爽了

#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=1e5+5;

int abs(int x){return x>0?x:-x;}

struct point{
    int x,y,idx,idy,mid;
    bool operator <(const point&aa)
        const {return mid<aa.mid;}
}a[maxn];

int b[maxn*2],l,len,k,n;
ll ans;

void prepare(){
    for(int i=1;i<=l;i++)
        b[++len]=a[i].x,b[++len]=a[i].y;
    sort(b+1,b+len+1);
    for(int i=1;i<=l;i++){
        if(a[i].x>a[i].y) swap(a[i].x,a[i].y);
        a[i].idx=lower_bound(b+1,b+len+1,a[i].x)-b;
        a[i].idy=lower_bound(b+1,b+len+1,a[i].y)-b;
    }
}

int S1[maxn*2],S2[maxn*2];

int lowbit(int o){return o&-o;}
int add(int o,int k,int* C){
    while(o<=len){
        C[o]+=k;
        o+=lowbit(o);
    }
}

int find(int k,int *C){
    int ret=0,cnt=0;
    for(int i=17;i>=0;i--){
        ret+=(1<<i);
        if(ret>len||cnt+C[ret]>=k) ret-=(1<<i);
        else{
            cnt+=C[ret];
        }
    }
    return ret+1;
}

ll solve(){
    ll ans1=0,ans2=0,ansx=0;
    prepare();
    int A=0,B=b[len/2+1];
    for(int i=1;i<=len;i++)
        ans2+=abs(B-b[i]);
    for(int i=1;i<=l;i++)
        add(a[i].idx,1,S2),add(a[i].idy,1,S2);
    ansx=ans2;
    
    for(int i=1;i<=l;i++){
        int l1=i*2,l2=len-i*2;
        add(a[i].idx,1,S1);add(a[i].idy,1,S1);
        add(a[i].idx,-1,S2);add(a[i].idy,-1,S2);
        
        ans2-=abs(a[i].x-B)+abs(a[i].y-B);
        A=b[find(l1/2,S1)],B=b[find(l2/2+1,S2)];
        ans1+=abs(a[i].x-A)+abs(a[i].y-A);
        if(ans1+ans2<ansx) ansx=ans1+ans2;
    }
    return ansx;
}

int main(){
    char p,q;
    int u,v;
    scanf("%d%d",&k,&n);
    if(k==1){
        ans=n;
        for(int i=1;i<=n;i++){
            scanf("\n%c %d %c %d",&p,&u,&q,&v);
            if(p==q) ans+=abs(u-v),ans--;
            else b[++l]=u,b[++l]=v;
        }
        sort(b+1,b+l+1);
        int A=b[l/2];
        for(int i=1;i<=l;i++)
            ans+=abs(A-b[i]);
        printf("%lld\n",ans);
    }
    else{
        ans=n;
        for(int i=1;i<=n;i++){
            l++;
            scanf("\n%c %d %c %d",&p,&a[l].x,&q,&a[l].y);
            if(p==q) ans+=abs(a[l].x-a[l].y)-1,l--;
            else a[l].mid=a[l].x+a[l].y;
        }
        sort(a+1,a+l+1);
        printf("%lld",ans+solve());
    }
    return 0;
}

【数学建模】【APIO2015】Palembang Bridges

Description

Input

Output

Sample Input

Sample Output

HINT

题解

代码