标签:
我是一名初学者,如果你发现文中有错误,请留言告诉我,谢谢
如果需要检测到图像里面的边缘,首先我们需要知道边缘处具有什么特征。
对于一幅灰度图像来说,边缘两边的灰度值肯定不相同,这样我们才能分辨出哪里是边缘,哪里不是。
因此,如果我们需要检测一个灰度图像的边缘,我们需要找出哪里的灰度变化最大。显然,灰度变化越大,对比度越强,边缘就越明显。
那么问题来了,我们怎么知道哪里灰度变化大,哪里灰度变化小呢?
导数,梯度,边缘信息
在数学中,与变化率有关的就是导数。
如果灰度图像的像素是连续的(实际不是),那么我们可以分别原图像G对x方向和y方向求导数
![]() ,
,![]()
获得x方向的导数图像Gx和y方向的导数图像Gy。Gx和Gy分别隐含了x和y方向的灰度变化信息,也就隐含了边缘信息。
如果要在同一图像上包含两个方向的边缘信息,我们可以用到梯度。(梯度是一个向量)
原图像的梯度向量Gxy为(Gx,Gy),梯度向量的大小和方向可以用下面两个式子计算
![]()
![]()
角度值好像需要根据向量所在象限不同适当+pi或者-pi。
梯度向量大小就包含了x方向和y方向的边缘信息。
图像导数
实际上,图像矩阵是离散的。
连续函数求变化率用的是导数,而离散函数求变化率用的是差分。
差分的概念很容易理解,就是用相邻两个数的差来表示变化率。
下面公式是向后差分
x方向的差分:Gx(n,y) = G(n,y)-G(n-1,y)
y方向的差分:Gy(x,n) = G(x,n)-G(x,n-1)
实际计算图像导数时,我们是通过原图像和一个算子进行卷积来完成的(这种方法是求图像的近似导数)。
最简单的求图像导数的算子是 Prewitt算子 :
x方向的Prewitt算子为

y方向的Prewitt算子为
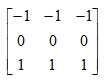
---------------------------------------------
原图像和一个算子进行卷积的大概过程如下
如果图像矩阵中一块区域为

那么x5处的x方向的导数是,将x方向算子的中心和x5重合,然后对应元素相乘再求和,即
x5处的x方向导数为x3+x6+x9-x1-x4-x7
对矩阵中所有元素进行上述计算,就是卷积的过程。
--------------------------------------------
因此,利用原图像和x方向Prewitt算子进行卷积就可以得到图像的x方向导数矩阵Gx,
利用原图像和y方向Prewitt算子进行卷积就可以得到图像的y方向导数矩阵Gy。
利用公式
![]()
就可以得到图像的梯度矩阵Gxy,这个矩阵包含图像x方向和y方向的边缘信息。
Python实现卷积及Prewitt算子的边缘检测
首先我们把图像卷积函数封装在一个名为imconv的函数中
import numpy as np from PIL import Image def imconv(image_array,suanzi): ‘‘‘计算卷积 参数 image_array 原灰度图像矩阵 suanzi 算子 返回 原图像与算子卷积后的结果矩阵 ‘‘‘ image = image_array.copy() # 原图像矩阵的深拷贝 dim1,dim2 = image.shape # 对每个元素与算子进行乘积再求和(忽略最外圈边框像素) for i in range(1,dim1-1): for j in range(1,dim2-1): image[i,j] = (image_array[(i-1):(i+2),(j-1):(j+2)]*suanzi).sum() # 由于卷积后灰度值不一定在0-255之间,统一化成0-255 image = image*(255.0/image.max()) # 返回结果矩阵 return image
然后我们利用Prewitt算子计算x方向导数矩阵Gx,y方向导数矩阵Gy,和梯度矩阵Gxy。
import numpy as np import matplotlib.pyplot as plt # x方向的Prewitt算子 suanzi_x = np.array([[-1, 0, 1], [ -1, 0, 1], [ -1, 0, 1]]) # y方向的Prewitt算子 suanzi_y = np.array([[-1,-1,-1], [ 0, 0, 0], [ 1, 1, 1]]) # 打开图像并转化成灰度图像 image = Image.open("pika.jpg").convert("L") # 转化成图像矩阵 image_array = np.array(image) # 得到x方向矩阵 image_x = imconv(image_array,suanzi_x) # 得到y方向矩阵 image_y = imconv(image_array,suanzi_y) # 得到梯度矩阵 image_xy = np.sqrt(image_x**2+image_y**2) # 梯度矩阵统一到0-255 image_xy = (255.0/image_xy.max())*image_xy # 绘出图像 plt.subplot(2,2,1) plt.imshow(image_array,cmap=cm.gray) plt.axis("off") plt.subplot(2,2,2) plt.imshow(image_x,cmap=cm.gray) plt.axis("off") plt.subplot(2,2,3) plt.imshow(image_y,cmap=cm.gray) plt.axis("off") plt.subplot(2,2,4) plt.imshow(image_xy,cmap=cm.gray) plt.axis("off") plt.show()
Prewitt算子 的结果如下图所示
上方:左图为原图像,右图为x方向导数图像
下方:左图为y方向导数图像,右图为梯度图像

从图中可以看出,Prewitt算子虽然能检测出图像边缘,但是检测结果较为粗糙,还带有大量的噪声。
近似导数的Sobel算子
Sobel算子与Prewitt比较类似,但是它比Prewitt算子要好一些。
x方向的Sobel算子为
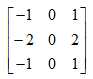
y方向的Sobel算子为

python代码只需要将上面代码中的Prewitt算子改成Sobel算子即可。
# x方向的Sobel算子 suanzi_x = np.array([[-1, 0, 1], [ -2, 0, 2], [ -1, 0, 1]]) # y方向的Sobel算子 suanzi_y = np.array([[-1,-2,-1], [ 0, 0, 0], [ 1, 2, 1]])
Sobel算子 的结果如下图所示
上方:左图为原图像,右图为x方向导数图像
下方:左图为y方向导数图像,右图为梯度图像

从图中看出,比较Prewitt算子和Sobel算子,Sobel算子稍微减少了一点噪声,但噪声还是比较多的。
未完,待续
参考列表
1.《python计算机视觉编程》
标签:
原文地址:http://www.cnblogs.com/smallpi/p/4555854.html