标签:
前言:
本人自接触算法近2年以来,在不断学习中越多地发觉各种算法中的美妙。之所以在这方面过多的投入,主要还是基于自身对高级程序设计的热爱,对数学的沉迷。回想一下,先后也曾参加过ACM大大小小的校级赛、区域赛。没什么惊天动地的奖项,最好的名次也就省三等奖。现在作为第一篇算法总结就拿常见的排序算法以我个人的理解,以及代码实现跟大家简单分享一下(排序算法如果一一罗列的话,不下十种。曾在图书馆的旧书架上看过一本近900页的书,内容就是专门介绍排序算法)。
选择排序(select)
选择排序比较容易理解,每一次往后遍历都是为了寻找“最小值”的下标。N次遍历,时间复杂度为:O(n^2)
冒泡排序(bubble)
冒泡排序也比较形象,理解为大气泡不断下沉,小气泡往上冒。同样往后进行n次遍历,时间复杂度为:O(n^2)。跟选择排序的区别:选择排序属于稳定排序,从初始状态到排序完成过程中的每一次遍历各元素前后位置“相对稳定”。而且,冒泡排序每一轮遍历可能产生多次交换swap(),而选择排序固定每一轮的遍历都只进行一次交换swap()操作。
插入排序(insert)
插入排序可以理解为对扑克牌排序,原先拿到一手杂乱的牌,通过“插入”将所有牌排好序。
一般的插入排序时间复杂度同样是:O(n^2),进行具体样例测试时跟样例数据的初始顺序有关。
希尔排序(shell)
希尔排序为进化版的插入排序,只因为其基于插入排序的思想上,加入步长”step”。一般读者可能不知道希尔排序应用到大量数据的排序的高效,据研究的学者表明一般情况下希尔排序的排序时间复杂度降低为O(n^(3/2))
归并排序(merge)
归并排序是基于递归的思想进行的一种时间复杂度为:O(N*lgN)排序算法,不过其附加O(n)的空间辅助代价。理解好归并排序后可以将其递归思想扩展应用到数列逆序数的求解问题上,这里不再展开。
快速排序(quick)
快速排序有多种实现方式,同样是利用递归的思想,不断将问题划分为具有相同性质的子问题进行求解。实现快速排序算法的平均时间复杂度为:O(N*lgN);快排的O(N*lgN)算法同样通过拓展可以用于求无序数列的“第K大”元素。
堆排序(heap)
二叉堆,简称堆(heap)。一种非常奇妙的数据结构,是本人接触过的算法当中最惊叹的算法之一,仅仅利用数组就可以实现。在堆排序中,我们一般采用大根堆,时间复杂度O(N*lgN),排序效果较快排稳定,而且也不需要额外的空间存储代价。
代码实现部分(C/C++),本程序建议在codeblocks这款界面比较友好的IDE测试。
1 /* 2 *排序算法汇总(C/C++实现) 3 */ 4 #include <cstdio> 5 #include <cstring> 6 //#define swap(x,y){x^=y;y^=x;x^=y;} 7 #define swap(x,y){int temp=x;x=y;y=temp;} 8 9 const int N = 10; 10 11 void selectSort(int *a,int n){ 12 for(int i=0;i<n;i++){ 13 int min=i; 14 for(int j=i+1;j<n;j++){ 15 if(a[j]<a[min]) min=j; 16 } 17 swap(a[i],a[min]); 18 } 19 } 20 //something error! 21 void bubbleSort(int *a,int n){ 22 for(int i=0;i<n;i++){ 23 for(int j=i;j<n;j++) 24 if(a[j]<a[i]) swap(a[i],a[j]); 25 } 26 } 27 void insertSort(int *a,int n){ 28 for(int i=1;i<n;i++){ 29 for(int j=i;j-1>=0&&a[j]<a[j-1];j--){ 30 swap(a[j],a[j-1]); 31 } 32 } 33 } 34 void shellSort(int *a,int n){ 35 //设定划分步长step 36 int step=3; 37 int h=1; 38 while(h*step<n) h=h*step + 1; 39 while(h>=1){ 40 for(int i=1;i<n;i++){ 41 for(int j=i;j-h>=0&&a[j]<a[j-h];j-=h) 42 swap(a[j],a[j-h]); 43 } 44 h /= step; 45 } 46 } 47 void mergeSort(int *a,int p,int q,int *T){ 48 //[p,q)左闭右开 49 if(p+1>=q) return; 50 int m = p+(q-p)/2; 51 //printf("m=%d\n",m); 52 mergeSort(a,p,m,T); 53 mergeSort(a,m,q,T); 54 for(int i=p,x=p,y=m;i<q;){ 55 if( x<m && y<q && a[x]<a[y] || y>=q) T[i++]=a[x++]; 56 else T[i++]=a[y++]; 57 } 58 for(int i=p;i<q;i++) 59 a[i] = T[i]; 60 } 61 void qSort(int *a,int p,int q){ 62 if(p>=q) return ; 63 int i=p-1; 64 for(int j=p;j<q;j++) if(a[j]<a[q]){ 65 i=i+1; 66 swap(a[i],a[j]); 67 } 68 i=i+1; 69 swap(a[i],a[q]); 70 71 qSort(a,p,i-1); 72 qSort(a,i+1,q); 73 } 74 75 void sink(int *a,int n,int k){ 76 while(2*k<=n){ 77 int j=2*k; 78 if(j<n && a[j]<a[j+1]) j++; 79 //if(a[j]<a[j+1]) j=j+1; 80 if(a[k] > a[j]) break; 81 swap(a[j],a[k]); 82 k = j; 83 } 84 } 85 void heapSort(int *a,int n){ 86 for(int k=n/2;k>=1;k--) 87 sink(a,n,k); 88 for(;n>1;){ 89 swap(a[1],a[n]); 90 n--; 91 sink(a,n,1); 92 } 93 } 94 void pt(int *a,int s,int n){ 95 for(int i=s;i<n;i++) 96 printf("%d ",a[i]); 97 printf("\n"); 98 } 99 int main(){ 100 //printf("Hello world!\n"); 101 int a[N]={2,1,-1,123,0,1,21,7,-10,1}; 102 int b[N+1]={-999,2,1,-1,123,0,1,21,7,-10,1}; 103 int T[N]; 104 int c; 105 printf("请选择一种排序算法:\n 1.选择排序\n 2.冒泡排序\n 3.插入排序\n 4.希尔排序\n 5.归并排序\n 6.快速排序\n 7.堆排序\n ----> "); 106 scanf("%d",&c); 107 switch(c){ 108 case 1: 109 selectSort(a,N); 110 break; 111 case 2: 112 bubbleSort(a,N); 113 break; 114 case 3: 115 insertSort(a,N); 116 break; 117 case 4: 118 shellSort(a,N); 119 break; 120 case 5: 121 mergeSort(a,0,N,T); 122 break; 123 case 6: 124 qSort(a,0,N-1); 125 break; 126 case 7: 127 heapSort(b,N); 128 break; 129 default: 130 printf("选择无效!"); 131 return 1; 132 } 133 printf("输出结果:\n"); 134 if(c==7) 135 pt(b,1,N+1); 136 else 137 pt(a,0,N); 138 139 return 0; 140 }
测试演示:
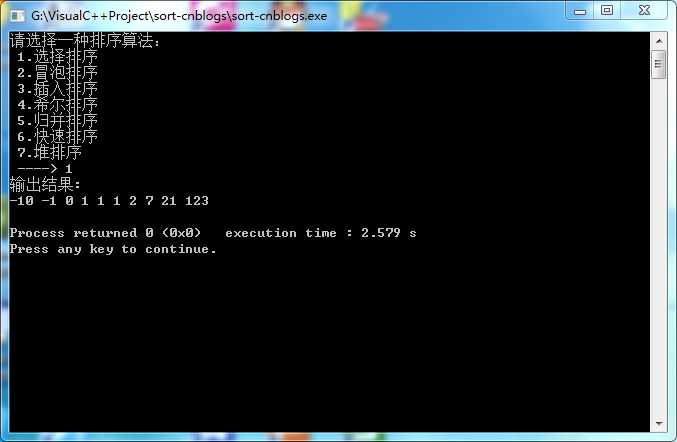
结语:
以上排序算法尚不能涵盖所有排序算法,比如基数排序,字符串排序等。本次排序算法分享内容就此打住,往后将持续更新。。。(因水平有限错漏在所难免,望各朋友不吝批评指正^_^)
标签:
原文地址:http://www.cnblogs.com/SeaSky0606/p/4559990.html