hihoCoder #1175 : 拓扑排序·二

标签：acm   hihocoder 拓扑排序   

【题目链接】：click here~~

描述

小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论，当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中，小Hi和小Ho整理得到了以下的信息：

• 校园网主干是由N个节点(编号1..N)组成，这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v，则节点u可以向节点v发送信息，但是节点v不能通过该链接向节点u发送信息。
• 在刚感染病毒时，校园网立刻切断了一些网络链接，恰好使得剩下网络连接不存在环，避免了节点被反复感染。也就是说从节点i扩散出的病毒，一定不会再回到节点i。
• 当1个病毒感染了节点后，它并不会检查这个节点是否被感染，而是直接将自身的拷贝向所有邻居节点发送，它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
• 现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。

举个例子，假设切断部分网络连接后学校网络如下图所示，由4个节点和4条链接构成。最开始只有节点1上有病毒。

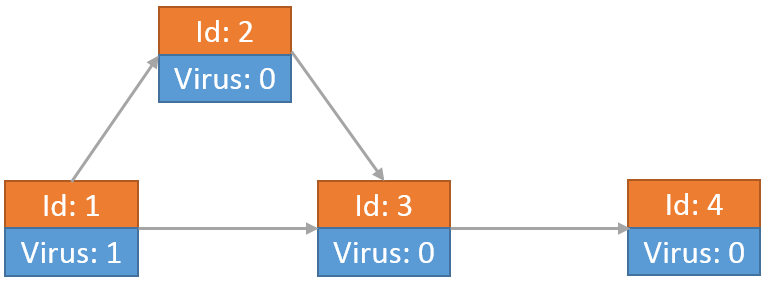
最开始节点1向节点2和节点3传送了病毒，自身留有1个病毒：

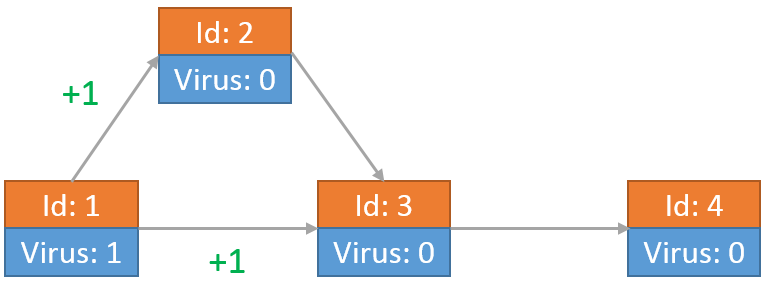
其中一个病毒到达节点2后，向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝：

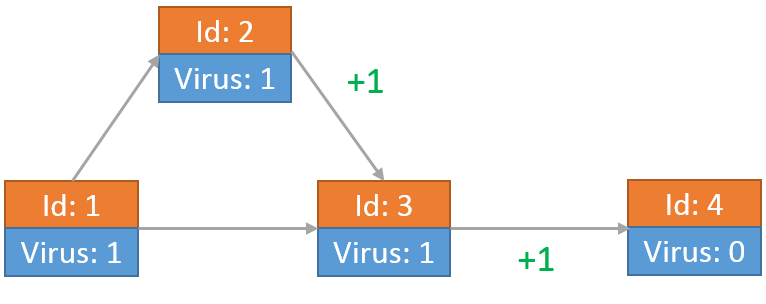
当从节点2传送到节点3的病毒到达之后，该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒：

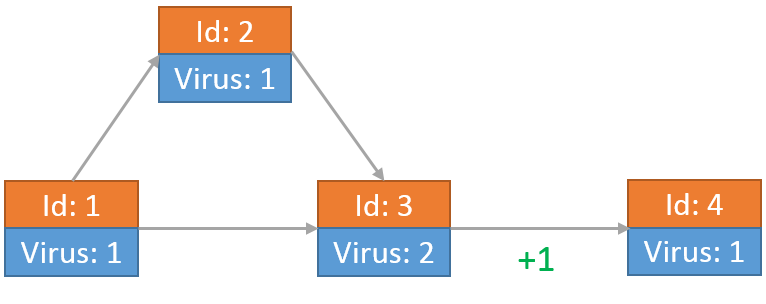
最后每个节点上的病毒为：

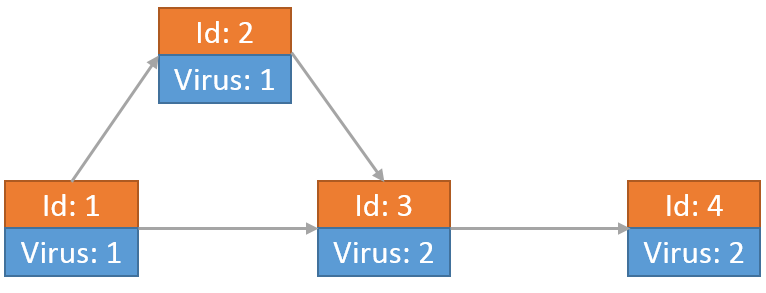
小Hi和小Ho根据目前的情况发现一段时间之后，所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说，最后会有多少个病毒呢？

提示：拓扑排序的应用

输入

第1行：3个整数N,M,K，1≤K≤N≤100,000，1≤M≤500,000

第2行：K个整数A[i]，A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N

第3..M+2行：每行2个整数 u,v，表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N

输出

第1行：1个整数，表示最后整个网络的病毒数量 MOD 142857

样例输入

4 4 1
1
1 2
1 3
2 3
3 4

样例输出

6

对于一个节点i来说，如果我们能够先计算出它所有前驱节点的病毒数量，就可以直接推算出它最后的病毒数量了，但是怎么来计算所有前驱节点呢？

这就要从图的性质入手了。我们现在的网络是没有环的，对于任意一个节点i，当它将自己所有的病毒都传送出去之后，它自身的病毒数量就不会改变了。那么我们不妨从没有前驱节点，也就是入度为0的节点开始考虑。

对于这些节点，它并不会再增加病毒数量。那么我们就根据它所关联的连接将病毒分发出去，然后这个节点就没有作用了。那不妨就删掉好了，它所关联的边也删掉，这样图中又会产生一些新的没有入度的节点。这样一直删点，直到所有的点都被删掉，将所有点的病毒数量加起来就是总的病毒数。

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int MOD=142857;
const double eps=1e-8;
const double inf=1e10;
int t,n,k,m,x;
int father[N],V[N],indegree[N];
vector <int >vec[N];
bool topsort()
{
    queue<int >q;
    while(!q.empty()) q.pop();
    for(int i=1; i<=n; i++)
        if(indegree[i]==0) q.push(i);
    int ans=0,sum=0;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        //sum++;
        ans+=V[u];
        ans%=MOD;
        for(int i=0; i<vec[u].size(); i++)
        {
            int temp=vec[u][i];
            V[temp]+=V[u];
            V[temp]%=MOD;
            if(--indegree[temp]==0) q.push(temp);
        }
    }
    printf("%u\n",ans);
    /*
    if(sum<n) return false;判断拓扑排序
    return true;
    */
}
int main()
{
    int u,v,a;
    while(scanf("%d%d%d",&n,&m,&k)!=EOF)
    {
        memset(indegree,0,sizeof(indegree));
        for(int i=1;i<=n;i++) if(vec[i].size()) vec[i].clear();
        for(int i=1; i<=k; i++) { scanf("%d",&v); V[v]++;}
        while(m--)
        {
            scanf("%d%d",&v,&u);
            vec[v].push_back(u);
            indegree[u]++;
        }
        /*
        if(topsort()) puts("YES");
        else puts("NO");
        */
        topsort();
    }
    return 0;
}

hihoCoder #1175 : 拓扑排序·二

标签：acm   hihocoder 拓扑排序   

原文地址：http://blog.csdn.net/u013050857/article/details/46411929