算法学习笔记：最大连续子数组

标签：

寻找最大连续子数组

　　这两天看了看数据结构与算法，对其中一个问题颇感兴趣，所以在这里写一下。问题：寻找最大连续子数组。

　　问题：在一个有正有负的数组中，寻找一个连续的、和最大的子数组。这个数组类似于下面的数组，否则这个问题没有意义（如果全是正数的话，所有数组元素的和一定是最大的，同样全为负数也没有意义。）。

 int a={1,-2,3,45,-78,34,-2,6};

解法一：暴力求解。

　　那么如何来解决这个问题呢？这个思路要起来并不难，绝大多数人会想到这样的办法：遍历该数组的所有子数组，找到和最大的那个子数组即可。因为遍历一次需要O(N)这么多时间，而数组又有N个元素，所以这个方法所用的时间为O(N^2)。那么有没有更快一点的方法呢？有！

方法二：分治法。

　　分治法的意思就是“分而治之”。该方法把原问题分解为规模较小的子问题（一般为等分），这些子问题性质与原问题相同但是规模较小，求解这些子问题后合并这些子问题的解便得到了原问题的解。

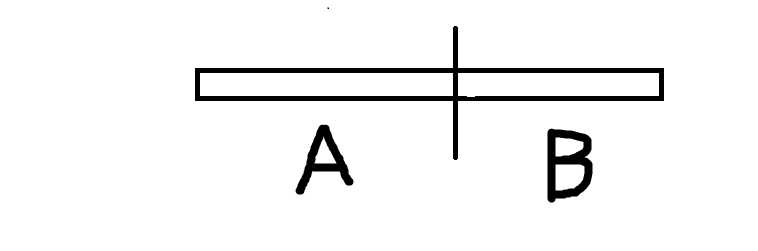
 　　 我们将数组一分为二：分划左为A，分划右为B。那么一个数组的最大连续子数组这有三种可能：全在A，全在B，横跨在分划线的两端。寻找A与B的任务与原来的任务相同，先不理会，先去寻找横跨的那个子数组。

FIND_MAX_CROSSING_ARRAY(A,low,mid,high)
left-sum=-无穷
find_left=0;
sum=0
for i=mid downto low
    if (sum+a[i]>sum)
        left_sum=sum
        find_left=i
sum=0;
right_sum=-无穷
find_right=0;
for i=mid+1 to high
    if (sum+a[i]>sum)
         right_sum=sum
         find_right=i
sum=left_sum+right_sum
return sum,find_left,find_right

　　以上就是寻找横跨最大连续子数组的伪代码。有了这个伪代码，我们就可以设计一个新的算法来寻找最大连续子数组。

FIND_MAX_ARRAY(A,low,high)
    if low==high
        return A[low],low,high
    else
        mid=(low+high)/2
        (left,left_low,left_high)=FIND_MAX_ARRAY(A,low,mid)
        (right,right_low,right_high)=FIND_MAX_ARRAY(A,mid+1,high)
        (mid1,mid_low,mid_high)=FIND_MAX_CROSSING_ARRAY(A,low,mid,high)
        //这样就分别找到了各自的最大连续子数组，找到三者最大返回即可
    比较三者，找到最大的那个。
    return (最大值,下标,上标)

　　这就是寻找最大子数组的伪代码了，通过分析发现时间复杂度为O(nlogn)。在渐进效率上击败了平凡算法。这就是利用分治法解决最大连续子数组的伪代码。

方法三：类动态规划

　　利用如下思维解决这个问题。

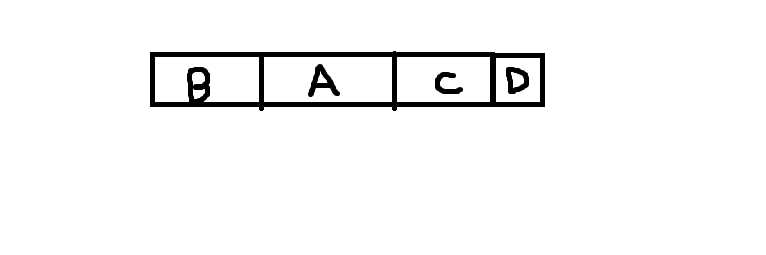
　　D为后来新加入的元素，A为原数组的最大部分而B、C是被抛弃的区域，显然B与C的和都小于零，否则A便不是最大的区域。此时加入了D之后，最大的连续子数组存在于三个情况之中：A，A+C+D,D，不会再出现其它的情况。可以在常量时间内解决。所以这也是个办法是线性时间的。

　　注意：在分治法中把数组一分为二可能遇到数组无法正好平分的情况，此时采取取整的策略。可以证明不会影响该算法的实施与时间复杂度。

算法学习笔记：最大连续子数组

标签：

原文地址：http://www.cnblogs.com/wufeng1234/p/4562619.html