hiho欧拉路·二 ----- Fleury算法求欧拉路径

hiho欧拉路·二

分析：

小Ho：这种简单的谜题就交给我吧！

小Hi：真的没问题么？

<10分钟过去>

小Ho：啊啊啊啊啊！搞不定啊！！！骨牌数量一多就乱了。

小Hi：哎，我就知道你会遇到问题。

小Ho：小Hi快来帮帮我！

小Hi：好了，好了。让我们一起来解决这个问题。

<小Hi思考了一下>

小Hi：原来是这样。。。小Ho你仔细观察这个例子：

因为相连的两个数字总是相同的，不妨我们只写一次，那么这个例子可以写成：3-2-4-3-5-1。6个数字刚好有5个间隙，每个间隙两边的数字由恰好对应了一块骨牌。

如果我们将每一个数字看作一个点，每一块骨牌看作一条边。你觉得是怎么样的呢？

小Ho：以这个例子来说的话，就是：

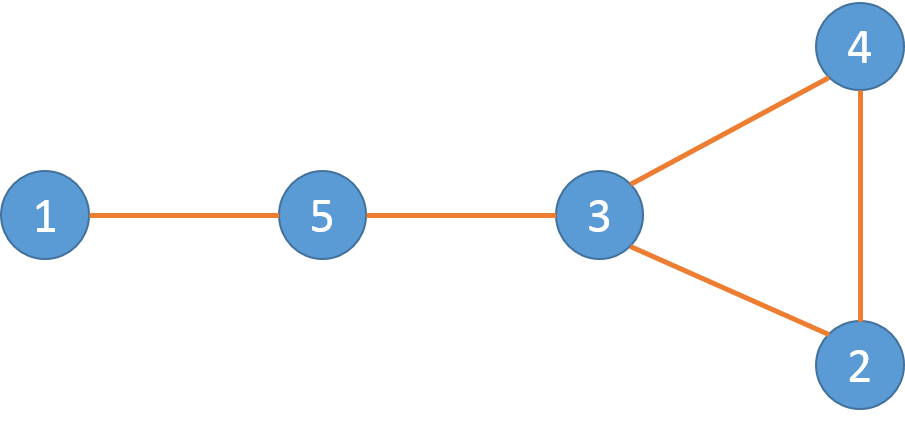
要把所有的骨牌连起来，也就是把所有的边都走一次。咦，这不是欧拉路问题么！

小Hi：没错，这问题其实就是一个欧拉路的问题，不过和上一次不一样的在于，这一次我们要找出一条欧拉路径。

小Ho：那我们应该如何来找一条路径呢？

小Hi：我们还是借用一下上次的例子吧

使用我们上一次证明欧拉路判定的方法，我们在这个例子中找到了2条路径：

L1: 4-5-2-3-6-5
L2: 2-4-1-2
假设我们栈S，记录我们每一次查找路径时的结点顺序。当我们找到L1时，栈S内的情况为：

S: 4 5 2 3 6 5 [Top]
此时我们一步一步出栈并将这些边删除。当我们到节点2时，我们发现节点2刚好是L1与L2的公共节点。并且L2满足走过其他边之后回到了节点2。如果我们在这个地方将L2先走一遍，再继续走L1不就刚好走过了所有边么。

而且在上一次的证明中我们知道，除了L1之外，其他的路径L2、L3…一定都满足起点与终点为同一个点。所以从任意一个公共节点出发一定有一条路径回到这个节点。

由此我们得到了一个算法：

在原图中找一个L1路径

从L1的终点往回回溯，依次将每个点出栈。并检查当前点是否还有其他没有经过的边。若存在则以当前点为起点，查找L2，并对L2的节点同样用栈记录重复该算法。

当L1中的点全部出栈后，算法结束。

在这里我们再来一个有3层的例子：

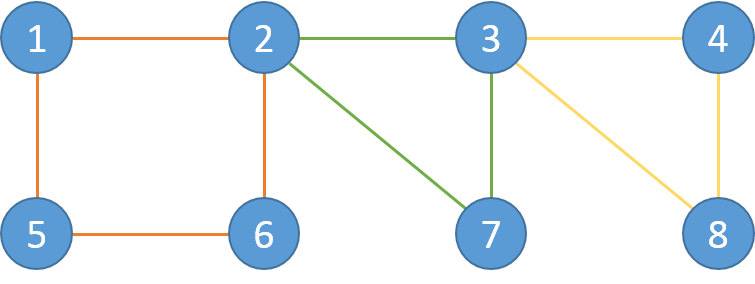
在这个例子中：

L1: 1-2-6-5-1
L2: 2-3-7-2
L3: 3-4-8-3
第一步时我们将L1压入栈S，同时我们用一个数组Path来记录我们出栈的顺序：

S: [1 2 6 5 1]
Path:
然后出栈到节点2时我们发现了2有其他路径，于是我们把2的另一条路径加入：

S: 1 [2 3 7 2]
Path: 1 5 6
此时L2已经走完，然后再开始弹出元素，直到我们发现3有其他路径，同样压入栈：

S: 1 2 [3 4 8 3]
Path: 1 5 6 2 7
之后依次弹出剩下的元素：

S:
Path: 1 5 6 2 7 3 8 4 3 2 1
此时的Path就正好是我们需要的欧拉路径。

小Ho：原来这样就能求出欧拉路，真是挺巧妙的。

小Hi：而且这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程，所以我们直接利用DFS的性质来实现栈，其伪代码如下：

**DFS(u):
While (u存在未被删除的边e(u,v))
删除边e(u,v)
DFS(v)
End
PathSize ← PathSize + 1
Path[ PathSize ] ← u**

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 1005;
int n, m, flag, top, sum, du[N], ans[5005], map[N][N];

void dfs(int x)
{
    ans[++top] = x;
    for(int i = 1; i <= n; i++)
    {
        if(map[x][i] >= 1)
        {
            map[x][i]--;
            map[i][x]--;
            dfs(i);
            break;
        }
    }
}

void fleury(int x)
{
    top = 1;
    ans[top] = x;
    while(top > 0)
    {
        int k = 0;
        for(int i = 1; i <= n; i++)//判断是否可扩展
        {
            if(map[ans[top]][i] >= 1)//若存在一条从ans[top]出发的边  那么就是可扩展
            {k = 1; break;}
        }
        if(k == 0)//该点x没有其他的边可以先走了（即不可扩展）， 那么就输出它
        {
            printf("%d ", ans[top]);
            top--;
        }
        else if(k == 1)//如可扩展， 则dfs可扩展的哪条路线
        {
            top--;//这需要注意
            dfs(ans[top+1]);
        }
    }
}
int main()
{
    while(scanf("%d%d", &n, &m) != EOF)
    {
        memset(du, 0, sizeof(du));
        memset(map, 0, sizeof(map));

        for(int i = 1; i <= m; i++)
        {
            int x, y;
            scanf("%d%d", &x, &y);
            map[x][y]++; //记录边， 因为是无向图所以加两条边， 两个点之间可能有多条边
            map[y][x]++;
            du[x]++;
            du[y]++;
        }
        flag = 1; // flag标记开始点。 如果所有点度数全为偶数那就从1开始搜
        sum = 0;
        for(int i = 1; i <= n; i++)
        {
            if(du[i] % 2 == 1)
            {
                sum++;
                flag = i;// 若有奇数边， 从奇数边开始搜
            }
        }
        if(sum == 0 || sum == 2)
            fleury(flag);
    }
    return 0;
}