标签:
简单易学的机器学习算法——EM算法
一、机器学习中的参数估计问题
在前面的博文中,如“简单易学的机器学习算法——Logistic回归”中,采用了极大似然函数对其模型中的参数进行估计,简单来讲即对于一系列样本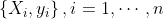 ,Logistic回归问题属于监督型学习问题,样本中含有训练的特征
,Logistic回归问题属于监督型学习问题,样本中含有训练的特征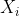 以及标签
以及标签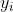 ,在Logistic回归的参数求解中,通过构造样本属于类别
,在Logistic回归的参数求解中,通过构造样本属于类别 和类别
和类别 的概率:
的概率:
=\sigma&space;\left&space;(&space;\theta&space;^TX&space;\right&space;))
=1-\sigma&space;\left&space;(&space;\theta&space;^TX&space;\right&space;))
这样便能得到Logistic回归的属于不同类别的概率函数:
=\left&space;(&space;\sigma&space;\left&space;(&space;\theta&space;^TX&space;\right&space;)&space;\right&space;)^y\left&space;(1-\sigma&space;\left&space;(&space;\theta&space;^TX&space;\right&space;)&space;\right&space;)^\left&space;(&space;1-y&space;\right&space;))
此时,使用极大似然估计便能够估计出模型中的参数。但是,如果此时的标签 是未知的,称为隐变量,如无监督的学习问题,典型的如K-Means聚类算法,此时不能直接通过极大似然估计估计出模型中的参数。
是未知的,称为隐变量,如无监督的学习问题,典型的如K-Means聚类算法,此时不能直接通过极大似然估计估计出模型中的参数。
二、EM算法简介
在上述存在隐变量的问题中,不能直接通过极大似然估计求出模型中的参数,EM算法是一种解决存在隐含变量优化问题的有效方法。EM算法是期望极大(Expectation Maximization)算法的简称,EM算法是一种迭代型的算法,在每一次的迭代过程中,主要分为两步:即求期望(Expectation)步骤和最大化(Maximization)步骤。
三、EM算法推导的准备
1、凸函数
设 是定义在实数域上的函数,如果对于任意的实数
是定义在实数域上的函数,如果对于任意的实数 ,都有
,都有

那么 是凸函数。若
是凸函数。若 不是单个实数,而是由实数组成的向量,此时,如果函数
不是单个实数,而是由实数组成的向量,此时,如果函数 的Hesse矩阵
的Hesse矩阵 是半正定的,即
是半正定的,即

那么 是凸函数。特别地,如果
是凸函数。特别地,如果 或者
或者 ,那么称
,那么称 为严格凸函数。
为严格凸函数。
2、Jensen不等式
如果函数 是凸函数,
是凸函数, 是随机变量,那么
是随机变量,那么
![E\left [ f\left ( x \right ) \right ]\geqslant f\left ( Ex \right ) 技术分享](http://latex.codecogs.com/gif.latex?E\left&space;[&space;f\left&space;(&space;x&space;\right&space;)&space;\right&space;]\geqslant&space;f\left&space;(&space;Ex&space;\right&space;))
特别地,如果函数 是严格凸函数,那么
是严格凸函数,那么![E\left [ f\left ( x \right ) \right ]= f\left ( Ex \right ) 技术分享](http://latex.codecogs.com/gif.latex?E\left&space;[&space;f\left&space;(&space;x&space;\right&space;)&space;\right&space;]=&space;f\left&space;(&space;Ex&space;\right&space;)) 当且仅当
当且仅当
=1)
即随机变量 是常量。
是常量。

(图片来自参考文章1)
注:若函数 是凹函数,上述的符号相反。
是凹函数,上述的符号相反。
3、数学期望
3.1随机变量的期望
设离散型随机变量 的概率分布为:
的概率分布为:
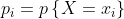
其中,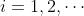 ,如果
,如果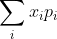 绝对收敛,则称
绝对收敛,则称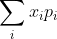 为
为 的数学期望,记为
的数学期望,记为) ,即:
,即:
=\sum_{i}x_ip_i)
若连续型随机变量 的概率密度函数为
的概率密度函数为) ,则数学期望为:
,则数学期望为:
=\int_{-\infty&space;}^{+\infty&space;}xf\left&space;(&space;x&space;\right&space;)dx)
3.2随机变量函数的数学期望
设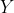 是随机变量
是随机变量 的函数,即
的函数,即) ,若
,若 是离散型随机变量,概率分布为:
是离散型随机变量,概率分布为:
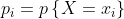
则:
=E\left&space;(&space;g\left&space;(&space;X&space;\right&space;)&space;\right&space;)=\sum_{i}g\left&space;(&space;x_i&space;\right&space;)p_i)
若 是连续型随机变量,概率密度函数为
是连续型随机变量,概率密度函数为) ,则
,则
=E\left&space;(&space;g\left&space;(&space;X&space;\right&space;)&space;\right&space;)=\int_{-\infty&space;}^{+\infty&space;}g\left&space;(&space;x&space;\right&space;)f\left&space;(&space;x&space;\right&space;)dx)
四、EM算法的求解过程
假设
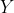
表示观测变量,
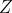
表示潜变量,则此时
)
即为完全数据,
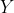
的似然函数为
)
,其中,

为需要估计的参数,那么对于完全数据,
)
的似然函数为
)
。
构建好似然函数,对于给定的观测数据,为了估计参数

,我们可以使用极大似然估计的方法对其进行估计。因为变量
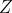
是未知的,我们只能对
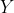
的似然函数为
)
进行极大似然估计,即需要极大化:
上述式子中无法直接对
)
求极大值,因为在函数中存在隐变量
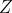
,即未知变量。若此时,我们能够确定隐变量
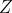
的值,便能够求出
)
的极大值,可以用过不断的修改隐变量
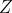
的值,得到新的
)
的极大值。这便是EM算法的思路。通过迭代的方式求出参数

。
首先我们需要对参数

赋初值,进行迭代运算,假设第

次迭代后参数

的值为
)
,此时的log似然函数为
\right&space;))
,即:
在上式中,第二行到第三行使用到了Jensen不等式,由于log函数是凹函数,由Jensen不等式得到:
而
表示的是
}&space;\right&space;)}{Q_i\left&space;(&space;Z&space;\right&space;)})
的期望,其中,
)
表示的是隐变量
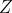
满足的某种分布。这样,上式
\right&space;))
的值取决于
)
和
}&space;\right&space;))
的概率。在迭代的过程中,调整这两个概率,使得下界不断的上升,这样就能求得
)
的极大值。注意,当等式成立时,说明此时已经等价于
)
。由Jensen不等式可知,等式成立的条件是随机变量是常数,即:
已知:
所以:
则:
至此,我们得出了隐变量
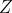
满足的分布的形式
)
。这就是EM算法中的E步。在确定了
)
后,调整参数

使得
)
取得极大,这便是M步。EM算法的步骤为:
- 初始化参数
) ,开始迭代;
,开始迭代;
- E步:假设
) 为第
为第 次迭代参数
次迭代参数 的估计值,则在第
的估计值,则在第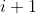 次迭代中,计算
次迭代中,计算) :
:=P\left&space;(&space;Z\mid&space;Y,\theta&space;^\left&space;(&space;i&space;\right&space;)&space;\right&space;))
- M步:求使
\right&space;)) 极大化的
极大化的 ,确定第
,确定第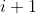 次的参数的估计值
次的参数的估计值) :
:}=\underset{\theta&space;}{arg\:&space;max}\sum_{Z}Q_i\left&space;(&space;Z&space;\right&space;)\cdot&space;log\;&space;\frac{P\left&space;(&space;Y,Z\mid&space;\theta&space;^\left&space;(&space;i&space;\right&space;)&space;\right&space;)}{Q_i\left&space;(&space;Z&space;\right&space;)})
五、EM算法的收敛性保证
迭代的过程能否保证最后找到的就是最大的似然函数值呢?即需要证明在整个迭代的过程中,极大似然估计是单调增加的。假定
)
和
)
是EM算法的第

次和第
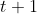
次迭代后的结果,选定
)
,进行迭代:
上式中,第一个大于等于是因为:
六、利用EM算法参数求解实例
假设有有一批数据) 分别是由两个正态分布:
分别是由两个正态分布:
)
)
产生,其中,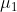 和
和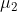 未知,
未知, 。但是不知道具体的
。但是不知道具体的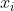 是第产生,即可以使用
是第产生,即可以使用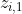 和
和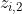 表示。这是一个典型的涉及到隐藏变量的例子,隐藏变量为
表示。这是一个典型的涉及到隐藏变量的例子,隐藏变量为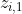 和
和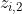 。可以使用EM算法对参数进行估计。
。可以使用EM算法对参数进行估计。
- 首先是初始化
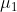 和
和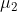 ;
;
- E步:
=P\left&space;(&space;Z\mid&space;Y,\theta&space;^\left&space;(&space;i&space;\right&space;)&space;\right&space;)) ,即求数据
,即求数据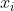 是由第
是由第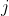 个分布产生的概率:
个分布产生的概率:=\frac{e^{-\frac{1}{2\sigma&space;^2}\left&space;(&space;x_i-\mu&space;_j&space;\right&space;)^2}}{\sum_{n=1}^{2}e^{-\frac{1}{2\sigma&space;^2}\left&space;(&space;x_i-\mu&space;_n\right&space;)^2}})
- M步:
}=\underset{\theta&space;}{arg\:&space;max}\sum_{Z}Q_i\left&space;(&space;Z&space;\right&space;)\cdot&space;log\;&space;\frac{P\left&space;(&space;Y,Z\mid&space;\theta&space;^\left&space;(&space;i&space;\right&space;)&space;\right&space;)}{Q_i\left&space;(&space;Z&space;\right&space;)}) ,即计算最大的期望值。然而我们要求的参数是均值,可以通过如下的方式估计:
,即计算最大的期望值。然而我们要求的参数是均值,可以通过如下的方式估计:x_i}{\sum_{i=1}^{m}P\left&space;(&space;z_{i,j}\mid&space;x_i,\mu&space;_j&space;\right&space;)})
Python代码
- ‘‘
- from __future__ import division
- from numpy import *
- import math as mt
- sigma = 6
- miu_1 = 40
- miu_2 = 20
-
- N = 1000
- X = zeros((1, N))
- for i in xrange(N):
- if random.random() > 0.5:
- X[0, i] = random.randn() * sigma + miu_1
- else:
- X[0, i] = random.randn() * sigma + miu_2
-
-
- k = 2
- miu = random.random((1, k))
- Expectations = zeros((N, k))
-
- for step in xrange(1000):
-
- for i in xrange(N):
-
- denominator = 0
- for j in xrange(k):
- denominator = denominator + mt.exp(-1 / (2 * sigma ** 2) * (X[0, i] - miu[0, j]) ** 2)
-
-
- for j in xrange(k):
- numerator = mt.exp(-1 / (2 * sigma ** 2) * (X[0, i] - miu[0, j]) ** 2)
- Expectations[i, j] = numerator / denominator
-
-
-
- oldMiu = zeros((1, k))
- for j in xrange(k):
- oldMiu[0, j] = miu[0, j]
- numerator = 0
- denominator = 0
- for i in xrange(N):
- numerator = numerator + Expectations[i, j] * X[0, i]
- denominator = denominator + Expectations[i, j]
- miu[0, j] = numerator / denominator
-
-
-
- epsilon = 0.0001
- if sum(abs(miu - oldMiu)) < epsilon:
- break
-
- print step
- print miu
-
- print miu
最终结果
[[ 40.49487592 19.96497512]]
参考文章:
1、(EM算法)The EM Algorithm (http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html)
2、数学期望(http://wenku.baidu.com/view/915a9c1ec5da50e2524d7f08.html?re=view)
简单易学的机器学习算法——EM算法
标签:
原文地址:http://www.cnblogs.com/yymn/p/4591766.html
,Logistic回归问题属于监督型学习问题,样本中含有训练的特征
以及标签
,在Logistic回归的参数求解中,通过构造样本属于类别
和类别
的概率:
是未知的,称为隐变量,如无监督的学习问题,典型的如K-Means聚类算法,此时不能直接通过极大似然估计估计出模型中的参数。
是定义在实数域上的函数,如果对于任意的实数
,都有
是凸函数。若
不是单个实数,而是由实数组成的向量,此时,如果函数
的Hesse矩阵
是半正定的,即
是凸函数。特别地,如果
或者
,那么称
为严格凸函数。
是凸函数,
是随机变量,那么
是严格凸函数,那么
当且仅当
是常量。
是凹函数,上述的符号相反。
的概率分布为:
,如果
绝对收敛,则称
为
的数学期望,记为
,即:
的概率密度函数为
,则数学期望为:
是随机变量
的函数,即
,若
是离散型随机变量,概率分布为:
是连续型随机变量,概率密度函数为
,则
分别是由两个正态分布:
和
未知,
。但是不知道具体的
是第产生,即可以使用
和
表示。这是一个典型的涉及到隐藏变量的例子,隐藏变量为
和
。可以使用EM算法对参数进行估计。