标签:
分治法的基本思想
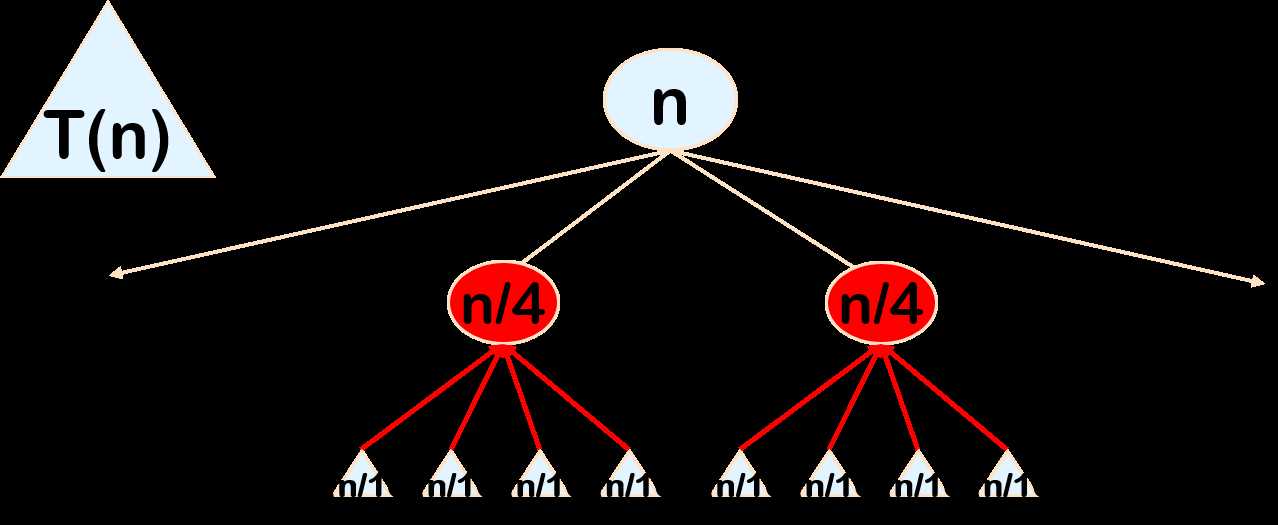
分治法是按照以下方案工作的:
1. 将问题的实例划分为同一个问题的几个较小的实例,最好拥有同样的规模。
2.对这些较小实例的求解(一般使用递归方法,但在问题规模足够小的时候,有时也会使用一些其他方法)。
3.如果必要的话,合并这些较小问题的解,以得到原始问题的解。
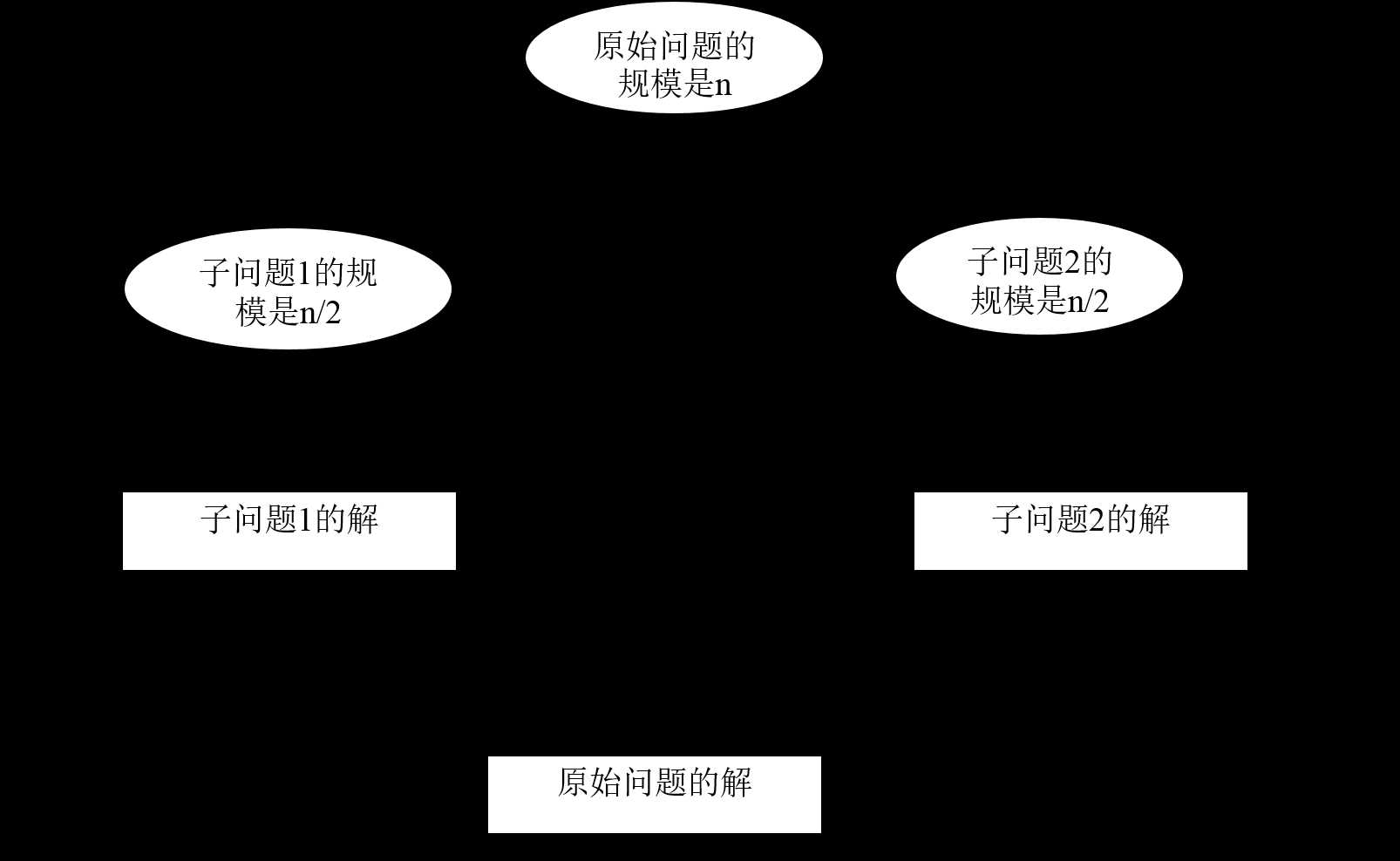
分治法一定能降低复杂度?获取高效率?
A0+A1+A2+….+An
(A0+….+A[n/2])+(A[n/2+1]+….+An)
T(n)=a T(n/b)+f(n)

例如,对于上面的分治法求和算法,当输入规模为n=2时,加法运算次数A(n)可以用下面的例子来说,a=2, b=2, d=0;这样一来,因为a> bd 即 2>1,
A(n)∈Θ(nlogba) = Θ(nlog22) = Θ(n)
标签:
原文地址:http://www.cnblogs.com/wensonH/p/4603997.html