大话数据结构之一（绪论、算法）

标签：

数据结构绪论

数据结构是相互之间存在一种或多种特定关系的数据元素的集合

程序设计=数据结构+算法

数据结构事实上就是一门研究非数值计算的程序设计问题的操作对象，以及它们之间的关系和操作等相关问题的学科。

数据是描述客观事件的符号，是计算机中可以操作的对象，是能被计算机识别，并输入能计算机处理的符号集合，也就是说数据必须具备两个前提：

1. 可以输入到计算机中
2. 能被计算机程序处理

数据

数据元素是组成数据的、有一定意义的基本单位，在计算机中通常作为整体处理，也被称为记录

数据项：一个数据元素可以由若干个数据项组成

数据项是数据不可分割的最小单位

数据对象：是性质相同的数据元素的集合，是数据的子集

不同数据元素之间不是独立的，而是存在特定的关系，我们将这些关系称为结构

数据结构：是相互之间存在一种或多种特定关系的数据元素的集合

逻辑结构：是指数据对象中数据元素之间的相互关系。

• 集合结构:集合结构中的数据元素除了同属于一个集合外，它们之间没有其它关系
• 
• 线性结构：线性结构中的数据元素之间是一对一的关系
• 
• 树性结构：树性结构中的数据元素之间是一对多的层次关系
• 
• 图形结构：图形结构中的数据元素是多对多的关系
• 

物理结构：是指数据的逻辑结构在计算机中的存储结构。

• 顺序存储结构：是把数据元素存储在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的
• 
• 链式存储结构：是把数据元素存储在任意的存储单元里，这组存储单元可以是连续的，也可是不连续的。
• 

数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。

1. 原子类型：是不可再分解的基本类型
2. 结构类型：由若干个类型组合而成，是可以再分解的。 

抽象是指抽取出事物具有的普遍性的本质。（抽取的意义在于数据类型的数学抽象特性）

抽象数据类型（Abstract Data Type ADT）：是指一个数据模型及定义在该模型上的一组操作。

抽象数据类型体现了程序设计中问题分解、抽象和信息隐藏的特征。

算法

算法：是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

算法的特性

1. 输入：具有零个或多个输入
2. 输出：至少有一个或多个输出
3. 有穷性：在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成
4. 确定性：算法的每一个步骤都具有确定的含义，不会出现二义性
5. 可行性：算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限的次数完成

算法的设计要求

1. 正确性：至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案
2. 可读性：算法设计的另一个目的是为了全球阅读、理解和交流
3. 健壮性：当输入数据不合法时，算法也能够做出相关处理，而不是产生异常或莫名其妙的结果
4. 时间效率高和存储量低：设计算法应该在尽量满足时间效率高和存储量低的需求 

算法效率的度量方法

1. 事后统计方法：通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低（不科学、不准确）
2. 事前分析估算方法：在计算机程序编制前，依据统计方法对算法进行估算

程序在计算机运行的时间取决于以下因素：

1. 算法采用的策略、方法
2. 编译产生的代码质量
3. 问题的输入规模
4. 机器执行指令的速度

也就是说一个程序的运行时间依赖于算法的好坏和问题的输入规模，最终在分析程序的运行时间时，最重要的是把程序看成是独立于程序设计语言的算法或一系列的步骤

算法时间复杂度

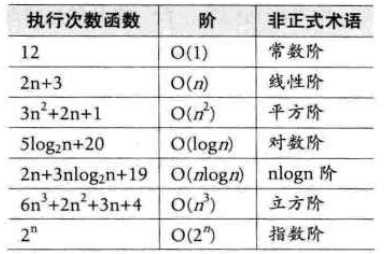
在判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项的阶数

如何分析一个算法的时间复杂度呢？方法就是：

常用时间复杂度分析

单纯的分支结构（不包含在循环结构中），其时间复杂度都是O(1)

分析算法的复杂度，关键是要分析循环结构的运行情况

纯性阶

            int i;
            for (i = 0; i < n; i++)//时间复杂度为O(n)
            { }

对数阶

            int count = 1;
            while (count<n)//由于count乘2之后，就距离n更近了一步，也就是2的x次方等于2 x=log2的n
                //所以时间复杂度为O(logn)
            {
                count = count * 2;
            }

平方阶

            int i, j;
            for (i = 0; i < n; i++)//时间复杂度为O(n的平方)
            {
                for (j = 0; j < n; j++)
                {
                    /*这里面的代码为时间复杂度为O(1)的程序步骤序列*/
                }
            }

分析一个相对复杂一点儿的......

        void fuc(int cout)//这个函数的时间复杂度为O(n)
        {
            for (int j = 0; j < n; j++)
            {
                /*这里面的代码为时间复杂度为O(1)的程序步骤序列*/
            }
        }
            n++;//执行次数为1
            fuc(n);//执行次数为n
            for (i = 0; i < n; i++)
            {
                fuc(i);//整个的执行次数为n2
            }
            for (i = 0; i < n; i++)
            {
                for (j = 0; j < n; j++)//当i=0，内循环执行n 当i=1内循环执行n-1次...
                    //所以总的执行次数为n+(n-1)+(n-2)+....+1=(n+1)n/2
                {
                    /*这里面的代码为时间复杂度为O(1)的程序步骤序列*/
                }
            }

上述代码总的执行次数为1+n+n的平方+n(n+1)/2=3/2n的平方+3/2n+1所以最终的时间复杂度为O(n的平方)

常见的时间复杂度

最坏情况运行时间是一种保证，也就是说运行时间不会比最坏情况下运行更长了。

平均运行时间是所有情况中最有意义的，因为它是期望的运行时间

算法的空间复杂度

大话数据结构之一（绪论、算法）

标签：

原文地址：http://www.cnblogs.com/liyunhua/p/4621958.html