标签:
Hard-Margin的约束太强了:要求必须把所有点都分开。这样就可能带来overfiiting,把noise也当成正确的样本点了。
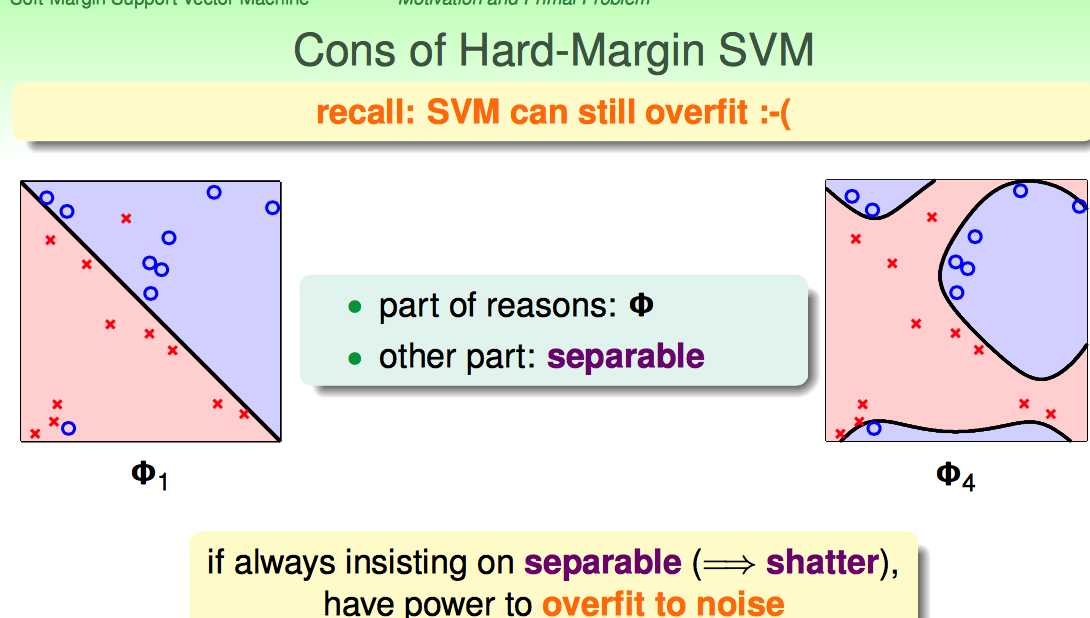
Hard-Margin有些“学习洁癖”,如何克服这种学习洁癖呢?

沿用pocket算法的思想,修改一下优化目标函数的形式,补上一个错分点的惩罚项CΣ...。
(1)C越大,对错误的容忍度就越小,margin越小
(2)C越小,对错误容忍度就越高,margin越大
因此引入的参数C是在large margin和noise tolerance之间做了一个权衡。
但是上面这种形式,有两个弊端:
(1)由于需要判断“等与不等”,所以是NP-hard Solution
(2)无法区分犯错点的错误程度
因此,引出了soft-margin的改进:

引入一个新的松弛因子kesi:
(1)既能解决学习洁癖的问题
(2)又能表示violation的程度是多少(kesi小于1还是分队的点,只不过此时点还在margin与hyperplane中间;kesi大于1表示分错了,越到hyperplance的另一端去了)
(3)还能转化成标准的QP问题,易于求解
接下来,沿用hard-margin dual svm的思路,把soft-margin SVM primal → dual。

由于不等式约束条件变成了两类,所以自然引入两个Largrange乘子;再沿用hard-margin的转化思路,转化成dual问题求解。
首先对kesi进行求导,化简原优化目标函数:

结论:
(1)利用对kesi求导为0的条件,把beta和kesi都去掉
(2)增加一个对alpha的约束条件

再进行接下来的化简,最终形式跟hard-margin很像。
不同之处在于对alpha增加了一个上界的约束条件。
一切看起来都比较顺利,但是在优化完成后,我们需要求解W和b。

W好求,问题的关键是b怎么求。


这里需要回顾KKT中的complementary slackness条件。
这里林直接给出来了,要free的那些SV(即满足kesi=0)来求解b;即对b求解有帮助的点,是真正在margin边界上的SV。
如果对之前SVM的complementary slackness内容不是很熟练,这块容易理解不好:为啥要分三类呢?下面记录下我的理解:
(1)当alphan=0的时候:
kesin必然等于0(为了满足(C-alphan)kesin=0)
【Soft-Margin Support Vector Machine】林轩田机器学习技术
标签:
原文地址:http://www.cnblogs.com/xbf9xbf/p/4622646.html