标签:
二路归并排序
归并排序采用了一种”分而治之“的策略:将原问题分解成N个规模较小而结构与原问题相似的子问题;递归求解这些子问题,然后合并其结果,从而得到原问题的解。
分治模式一般遵循以下三个步骤:
分解(Divide):将原问题分解成若干子问题;
解决(Conquer):递归地求解各子问题。若子问题足够小,则直接求解;
合并(Combine):将子问题的解合并成原问题的解。
”二路归并"的算法也遵循以下三个步骤:
分解:将原序列中拥有的N个元素分解各含N / 2个元素的子序列;
解决:用合并排序法对两个子序列递归排序;
合并:合并两个已排序的子序列得到原序列的解。
#define INF numeric_limits<int>::max()
哨兵模式的二路归并排序:

void Merge(int arr[], int start, int mid, int rear) { int i,j; int m = mid - start + 1;// Including [start, mid] int n = rear - mid;// including (mid, rear] int* leftArr = new int[m + 1]; int* rightArr = new int[n + 1]; for (i = 0; i < m; i++) leftArr[i] = arr[start + i]; for (j = 0; j < n; j++) rightArr[j] = arr[mid + j + 1]; leftArr[m] = INF;// 用了哨兵 rightArr[n] = INF; i = j = 0; for (int k = start; k <= rear; k++) { if (leftArr[i] < rightArr[j]) { arr[k] = leftArr[i++]; } else { arr[k] = rightArr[j++]; } } cout << "Merging ==> "; show(arr, 6); delete[] leftArr; delete[] rightArr; } void MergeSorting(int arr[], int start, int rear) { if (start < rear) { int mid = (start + rear) / 2; cout << "middle is: " << mid << endl; MergeSorting(arr, start, mid); MergeSorting(arr, mid + 1, rear); Merge(arr, start, mid, rear); show(arr, 6); } else { return; } }
不用哨兵实现的二路归并排序:

void Merge2(int arr[], int start, int mid, int rear) { int i,j, k; int m = mid - start + 1;// Including [start, mid] int n = rear - mid;// including (mid, rear] int* leftArr = new int[m]; int* rightArr = new int[n]; for (i = 0; i < m; i++) leftArr[i] = arr[start + i]; for (j = 0; j < n; j++) rightArr[j] = arr[mid + j + 1]; i = j = 0; for (k = start; i < m && j < n; k++) { if (leftArr[i] < rightArr[j]) { arr[k] = leftArr[i++]; } else { arr[k] = rightArr[j++]; } } if (i < m) for (int x = 0; x < m - i; x++) arr[k++] = leftArr[i + x]; if (j < n) for (int y = 0; y < n - j; y++) arr[k++] = rightArr[j + y]; cout << "Merging ==> "; show(arr, 6); delete[] leftArr; delete[] rightArr; } void MergeSorting2(int arr[], int start, int rear) { if (start < rear) { int mid = (start + rear) / 2; cout << "middle is: " << mid << endl; MergeSorting2(arr, start, mid); MergeSorting2(arr, mid + 1, rear); Merge2(arr, start, mid, rear); show(arr, 6); } else { return; } }
测试代码:

int main() { int a[] = { 1, 4, 2, 7, 10, 5 }; //insertion_sort_asc(a, 6); //insertion_sort_asc_with_while(a, 6); //insertion_sort_des(a, 6); MergeSorting2(a, 0, 5); return 0; }
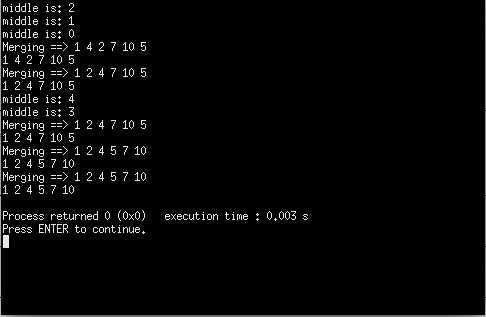
结果:
标签:
原文地址:http://www.cnblogs.com/AmitX-moten/p/4623148.html