| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 13765 | Accepted: 5760 |
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
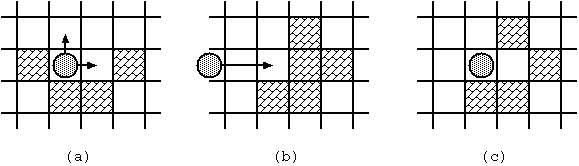
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
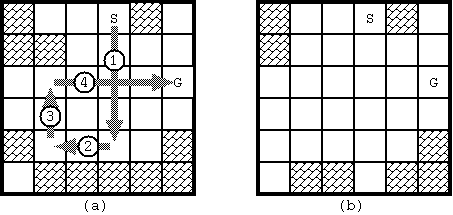
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
Source
题目链接:http://poj.org/problem?id=3009
题目大意:一个有n*m个格子的迷宫,一个小球从起点2出发,3为终点,0为空白格可以走,只能横竖走,1为障碍物,若小球碰到障碍物(走到与1相邻的格子),此处障碍物变为0,小球可改变方向。求小球抵达终点需改变方向的最少次数。若不能抵达终点,输出-1。
解题思路:BFS和DFS都可以做,用DFS需要比较每个答案得到最小值。如果改变方向次数大于10次或者大于已得到的答案值,则不需要在往后递归。
代码入下:
#include <cstdio>
#include <cstring>
int a[22][22];
int dx[4]={0,1,0,-1};//枚举4个方向
int dy[4]={-1,0,1,0};
int n,m,ans;
bool p;
void dfs(int x,int y,int cnt)
{
for(int i=0;i<4;i++)
{
int cx=x,cy=y,step=0;//step用来标记小球是否走了一段直线,若不走,下一个1不能变为0
//满足条件时按一个固定的方向走直线
while(cx+dx[i]>=0&&cx+dx[i]<n&&cy+dy[i]>=0&&cy+dy[i]<m&&a[cx+dx[i]][cy+dy[i]]==0)
{
cx+=dx[i];
cy+=dy[i];
step++;
}
if(cx+dx[i]<0 || cx+dx[i]>=n || cy+dy[i]<0 || cy+dy[i]>=m)
continue;
//小球抵达终点,比较得到最小答案值
if(a[cx+dx[i]][cy+dy[i]]==3)
{
p=true;
if(ans>cnt+1)
ans=cnt+1;
return;
}
//小球碰到障碍物
//如果改变方向次数大于10次或者大于已得到的答案值,则不需要在往后递归。
if(step&&ans>cnt+1&&cnt<10&&a[cx+dx[i]][cy+dy[i]]==1)
{
a[cx+dx[i]][cy+dy[i]]=0;
dfs(cx,cy,cnt+1);
a[cx+dx[i]][cy+dy[i]]=1;
}
}
}
int main()
{
int sx,sy;
while(scanf("%d%d",&m,&n)!=EOF&&(n+m))
{
p=false,ans=10000000;
memset(a,0,sizeof(a));
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
scanf("%d",&a[i][j]);
if(a[i][j]==2)
{
sx=i;
sy=j;
a[i][j]=0;
}
}
dfs(sx,sy,0);
if(p&&ans<=10)
printf("%d\n", ans);
else
printf("-1\n");
}
}版权声明:本文为博主原创文章,未经博主允许不得转载。
原文地址:http://blog.csdn.net/criminalcode/article/details/46813797