标签:
1.插入排序
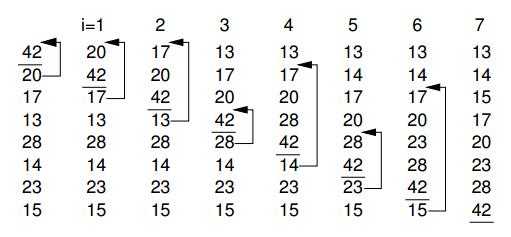
插入排序时最容易理解的排序方法,个人总结有三个关键点:
1. 需要将处理的元素暂时存储起来
2. j变量的范围控制
3. 插入值与j变量控制范围中元素大小的比较
相关代码:
1 //插入排序
2 template<class T> void sort(T* array, int n)
3 {
4 for (int i = 1; i < n; i++)
5 {
6 T temp = array[i]; //控制j的范围
8 for (int j = i; j > 0 && array[j - 1] > temp; j--) //在范围内进行比较
9 {
10 array[j] = array[j - 1];
11 }
12 array[j] = temp;
13 }
14 }
---------------------------------------------

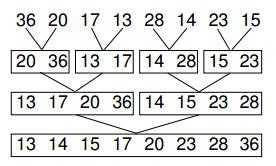
1 template<class T> void merge(T* a, int n1, int n2)
2 {
3 T* temp = new T[n1+n2];
4 int i =0;
5 int j1=0;
6 int j2=0;
7 //若左段,右段均在区域内,则选择小的填入新数组中
8 while (j1 < n1 && j2 < n2)
9 {
10 temp[i++] = ( a[j1] <= a[n1+j2] ? a[j1++] : a[n1+j2++] );
11 }
12 //若右段填完,左段有空余,则将左段所有填入新数组
13 while (j1 < n1)
14 {
15 temp[i++] = a[j1++];
16 }
17 //若左段填完,右段有空余,则将左段所有填入新数组
18 while (j2 < n2)
19 {
20 temp[i++] = a[n1+j2++];
21 }
22
23 for (i=0; i < n1+n2; i++)
24 {
25 a[i] = temp[i];
26 }
27 delete [] temp;
28 }
29 template<class T> void sort(T* a, int n)
30 {
31 if (n > 1)
32 {
33 int n1 = n/2;
34 int n2 = n - n1;
35 sort(a, n1);
36 sort(a+n1, n2);
37 merge(a, n1, n2);
38 }
39 }
---------------------------------------------------
The Shell Sort
---------------------------------------------------

// The Shell Sort templat<class T> void sort(T* a, int n) { int d = 1; int j = 0; //设定j为全局变量 //首先确定跳跃的距离,根据不同的长度的数组有不同的跳跃距离 while (d<n/9) { d = 3*d + 1; } while (d>0) //做跳跃增量插入排序 { for (int i=d; i<n; i++) { T t = a[i]; //将需要被插的数显保存 j=i; while (j>=d && a[j-d]>t) { a[j] = a[j-d]; j -= d; } a[j] = t; } d /= 3; 减少增量大小,继续做插排 } }
-------------------------------------------------------------
The Heap Sort (堆排序)
-------------------------------------------------------------
堆排序最重要的就是建立堆
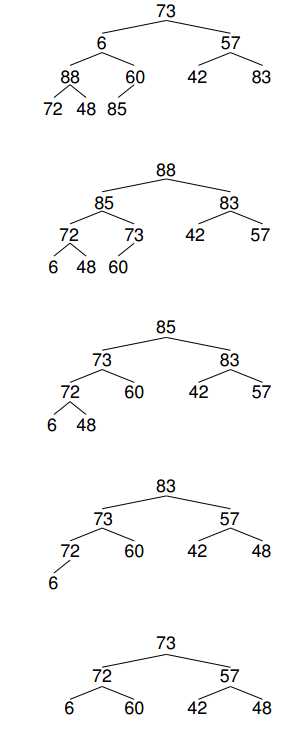
template<class T> void sort(T* a, int n) //非叶子节点都需要进行heapify,n为数组元素数量 { for (int i= n/2 - 1; i >=0; i--) heapify(a, i , n); for (int i = n-1; i > 0; i--) {
swap(a[0], a[i]); //先交换 // Invariant: the elements a[i:n-1] are in correct positions. heapify(a, 0 , i); //后建堆 // Invariant: the subarray a[0:i-1] has the heap property } } //建堆的方法依赖于数组中序号的互相关系 //在堆中元素K的子元素为2k+1和2k+2,k的父元素为(k-1)/2 template <class T> void heapify(T* a, int k, int n) {
T t = a[k]; while (k < n/2) {
int j = 2*k + 1; // 定位到左子结点 if (j+1 < n && a[j] < a[j+1]) ++j; //若有右子结点,且右大于左边 if (t > a[j]) break; //比较父节点与子节点大小 //此处隐藏有一级子节点必然都大于二级及三级子节点 a[k] = a[j]; k = j; } a[k] = t; }
-----------------------------------------------------
快排
-----------------------------------------------------
template<class T> void quickSort(T* a, int lo, int hi) { if (lo >= hi) return; T pivot = a[hi]; //确定Pivot int i = lo - 1; //定位左边初始位置,为-1即第一个元素前一个 int j = hi; //由于最后一个是Pivot所以其实也是空的 while (i < j) { while (a[++i] < pivot) ; //移动左边,注意先移动位置,后比较大小 while (j >= 0 && a[--j] > pivot) ; //移动右边,先移动位置后比较大小并确保j>0 if (i < j)
swap(a[i], a[j]); //交换元素,左右停止的位置 } swap(a[i], a[hi]); //交换左边与pivot quicksort(a, lo, i-1); //左边起始到pivot前一个元素 quicksort(a, i+1, hi); //pivot后一个到右边 } template<class T> void sort(T* a, int n) { quicksort(a, 0, n-1); }
标签:
原文地址:http://www.cnblogs.com/LauenWang/p/4152203.html