标签:
排序算法包括插入排序、选择排序、冒泡排序、快速排序、归并排序以及基数排序等六种,下面我们将从他们各自的原理、实现、时间与空间复杂度以及稳定性等方面进行分析。
1. 插入排序
基本思想:将一个记录插入到已排序好的有序表中,从而得到一个新的记录数增1的有序表。当表中只有一个数时当然是有序的,因此我们从第二的数开始实现插入算法。我们先看一下实现代码:
1 void InsertSort(vector<int>& a) 2 { 3 int n = a.size(); 4 int i, j; 5 for (i = 1; i < n; i++) 6 if (a[i] < a[i - 1]) 7 { 8 int temp = a[i]; 9 for (j = i - 1; j >= 0 && a[j] > temp; j--) 10 a[j + 1] = a[j]; 11 a[j + 1] = temp; 12 } 13 }
该过程实际上跟打扑克牌时摸排后的插牌过程是一个故事(当然哪些不安常理插排的人除外),如果我们给a初始化:a{5,4,8,7,3}.这好比你得到先后五张牌: 5 、 4 、8、7、3.
第5行中的循环 第一次i = 1 ,表示当你摸到第二张牌时开始考虑它的插入问题,很显然你要将它插到5之前,即满足第6行的判断条件。那要将其插到哪个,我们可以将其与它的前一个数比较,如果比前一个数小就将前一个数向后移动一位,为它的插入留出空间,同理然后继续与前前一个比较。那到什么时候结束呢?第9行中的判断条件:直到前一个数大于或等于它,又或者前面已没有数。在这里即j==-1时循环跳出,最后将新纪录数插入,见第11行,4被插到5的前面。当然为了避免插入数被前一个数移动后覆盖,要先将其保存在一个变量中,见第8行。
接着继续循环 i = 2,因为8比5大不满足第6行的条件,即8在原地不移动,即直接插到5的后面。继续循环,7要比8小满足第6行条件,将8向后移动一位,7继续与前一位比较,因为7比5小,所以内部循环结束,将7插到5的后面。继续循环,3比它前面所有数都小,最后内部循环跳出条件为j ==-1,因此将3插到第一位,到此整个过程结束,得到有序表{3,4,5,7,8}.
下面分析该算法的时间与空间复杂度:
因为整个过程只使用了一个临时变量保存被插入值,空间复杂度为O(1).
当最好的情况,给定的是有序表,则每次循环都不会满足第6行的条件,因此没有发生移动,只进行了n-1次比较,时间复杂度为O(n)。
因此对于一些本身就基本有序的和数据量比较小的,使用插入排序比较有优势。
当最坏的情况,给定的是逆序表,则每次都将它前面的所有元素向后移动一位,移动次数为1+2+...+n-1=(n-1)n/2,比较次数为2+3+...+n = (n-1)(n+2)/2. 如果排序是随机的,则平均的比较和移动次数为n^2/4, 因此时间复杂度为O(n^2).
从上面的比较过程中看出,碰见一个和插入元素相等的数时,直接把插入元素插入该数的后面。所以,相等元素的前后顺序没有改变,所以插入排序是稳定的。
在上面提到当记录本身就基本有序的和数据量比较小时,插入排序效率高,当这个条件很难满足,为了创造这样的条件,将相距某个增量的记录组成一个子序列,将每个子序列实现插入排序,这便是希尔排序。
1 void ShellSort(vector<int>& a) 2 { 3 int n = a.size(); 4 int i, step; 5 for (step = n / 2; step > 0; step /= 2) 6 { 7 for (i = step; i < n; i++) 8 { 9 if (a[i - step]>a[i]) 10 { 11 int temp = a[i]; 12 int k = i - step; 13 while (k >= 0 && a[k] > temp) 14 { 15 a[k + step] = a[k]; 16 k -= step; 17 } 18 a[k + step] = temp; 19 } 20 } 21 } 22 }
从第7行到第18行,这整个过程基本上就是一个插入排序,区别是之前是与前一个数比较,而这里是与子序列的前一个数比较,这子序列相距step,即前step个数比较,完成子序列的排序。每次插入排序完成后,便减小子序列的距离,一直到减为1,此时便是一个标准的插入排序。我们给定一个记录a{49,38,65,97,76,13,27,49,55,4},第一次我们使用的距离step = 10/2 = 5,子序列为{49,13}、{38,27}
{65,49}、{97,55}、{76,4},经过一次排序后得到{13,27,49,55,4,49,38,65,97,76};第二次使用距离step = 5 /2 =2,子序列为
{13,49,4,38,97}、{27,55,49,65,76},排序后得到{4,27,13,49,38,55,49,65,97,76},最后一次距离step = 2/2=1,此时成为一般的插入排序。
希尔排序的目的就是在数据量比较小或记录本身就基本有序的条件下进行插入排序,这种情况下的插入排序效率高,当step较大时,每个子序列数量小,二当step变大每个子序列数量变大后,经过之前的子序列排序,记录已满足基本有序的条件。希尔排序的时间复杂度与step 的选取有关,它的选取有多种方法,目前还没找到最佳方法。因为希尔排序有跳跃的调整数据顺序,因此它是不稳定的。
2. 选择排序
基本思想:首先从第一个数开始,将它与其他所有的数比较,找到最小的数将其放到第一个位置;然后再从第二个数开始,将它与剩下所有的数比较,找到最小的放到第二个位置,以此类推,最终将所有的数排好序。
1 void SelectSort(vector<int>& a) 2 { 3 int n = a.size(); 4 int i, j, nMinIndex; 5 for (i = 0; i < n; i++) 6 { 7 nMinIndex = i; //找最小元素的位置 8 for (j = i + 1; j < n; j++) 9 if (a[j] < a[nMinIndex]) 10 nMinIndex = j; 11 swap(a[i], a[nMinIndex]); //将这个元素放到无序区的开头 12 } 13 }
该算法过程比较简单,只需用一个变量记录最小元素的位置,空间复杂度为O(1).每次循环找到无序区的最小元素并将其放到无序区的开头位置。该算法的比较次数给定序列无关,都是 n-1+n-2+...+1=n(n-1)/2次,移动次数当为顺序时为0,为逆序时为n-1.所有该算法的时间复杂度为O(n^2),并且该算法是稳定的。
上述过程中每次循环只能确定一个值的位置,我们可以同时确定最大和最小值的位置,使得循环的次数减半。
1 void SelectSort1(vector<int>& a) 2 { 3 int n = a.size(); 4 int i, j, nMinIndex,nMaxIndex; 5 for (i = 0; i <= n/2; i++) 6 { 7 nMinIndex = i; nMaxIndex = i; //找最小,最大元素的位置 8 for (j = i + 1; j < n-i; j++) 9 { 10 if (a[j] < a[nMinIndex]) 11 { 12 nMinIndex = j; 13 continue; 14 } 15 if (a[j]>a[nMaxIndex]) 16 nMaxIndex = j; 17 } 18 if (i == nMaxIndex) 19 { 20 Exchange(a[n - 1 - i], a[nMaxIndex]); 21 Exchange(a[i], a[nMinIndex]); 22 } 23 else if (i == nMinIndex) 24 { 25 Exchange(a[n - 1 - i], a[nMaxIndex]); 26 } 27 else 28 { 29 Exchange(a[i], a[nMinIndex]); 30 Exchange(a[n - 1 - i], a[nMaxIndex]); 31 } 32 } 33 }
在这里注意不能将最小和最大值与无序列中的最前和最后位置进行交换,首先要判断最大值与最小值的位置是否与当前位置相同,如果最大值位置就是当前位置,只能先将最大值与最末位置元素交换,再将最小元素与当前位置交换,如果先交换最小元素与当前元素,进行最大值交换时又会将最小元素移动到最后位置。如果最小值位置就是当前位置,我们只需要交换最大值与最后一个元素即可。其他情况不用在意交换的先后。
选择排序中每一轮比较只选出了最小记录,而没有将比较过的结果记录下来,这样每一轮的比较可能会出现重复的情况,如果能将每次比较的结果记录下来,则能大大提高时间复杂度,这里使用堆排序。堆是拥有下列性质的完全二叉树:每个节点的值都大于或等于左右孩子节点的值,称为大顶堆;每个节点的值都小于或等于左右孩子节点的值,称为小顶堆;它可以由如下公式表示:
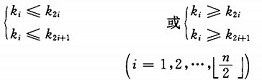
堆排序的思想:将待排序的序列构成一个大顶堆(也可以使用小顶堆,原理一样),将根节点与序列的最后位置的元素交换,此时便将最大值移到最后了;接着将剩余的n-1个元素再构成一个大顶堆,这样便得到第二大的元素。如此反复,最后得到一个有序的序列。
接下来的问题是如何构造堆,要保证每一个节点都满足堆的性质,从最后一个节点进行调整,然后反复进行此过程:
(1) n 个结点的完全二叉树,则最后一个结点是第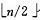 个结点的子树。因此从第
个结点的子树。因此从第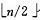 个结点为根的子树开始,该子树成为堆。
个结点为根的子树开始,该子树成为堆。
(2) 接着向前依次对各结点为根的子树进行筛选,使之成为堆,直到根结点。代码如下:
void Maxheap(vector<int>& a, int i) { int n = a.size(); int j, temp; temp = a[i]; j = 2 * i + 1; while (j < n) { if (j + 1 < n && a[j + 1] > a[j]) //在左右孩子中找最大的 j++; if (a[j]<=temp) break; a[i] = a[j]; //把较大的子结点往上移动,替换它的父结点 i = j; j = 2 * i + 1; } a[i] = temp; } void BuildHeap(vector<int>& a) { int r = a.size(); for (int i =r/2-1; i>=0; i--) Maxheap(a, i); }
建立堆之后,序列的第一个元素为最大值,将其与最后的元素交换,然后将其pop出序列,接着对序列中剩余的元素建堆。循环操作直到序列中只有一个元素,代码如下:
1 vector<int> HeapSort(vector<int>& a) 2 { 3 BuildHeap(a); 4 int length = a.size(); 5 vector<int> res(length, 0); 6 for (int i = length-1; i>=1; i--) 7 { 8 Exchange(a[i], a[0]); 9 res[i] = a[i]; 10 a.pop_back(); 11 Maxheap(a, 0); 12 } 13 res[0]=a[0]; 14 return res; 15 }
标签:
原文地址:http://www.cnblogs.com/zhulong890816/p/4659541.html