标签：
EM算法
看到别人的博客写得那么好，自己也不动于衷，于是，根据自己的理解也写一下。虽然写这么多字的博客很费劲，但是，这是自己重新组织和思考的一个过程，受益匪浅。大多根据自己的理解，如有错误，望批评指正，来世做牛做马。废话少说，马上进入正题。
这里，主要根据GMM模型来说明这个算法的。
一、为什么提出这个模型
在高中之前，对“确定数学”非常喜欢，而对“随机数学”这种不确定的东西非常厌恶。之所以厌恶，受到应试教育的影响——答案只有一个。随机数学之随机让人心有余悸。大学以来，通信专业的噪声不绝于耳，数学建模误差无处不在，让我知道随机数学的广泛应用，深深爱之。要知道，确定信号是随机信号中非常特殊的一种，随机才是“正道”。说得有些过分，目的是强调随机数学之强大。
既然如此，谈到随机数学，首先提到密度函数。知道密度函数就可以提高正确分类的概率。概率密度函数分为离散密度函数，连续密度函数。离散的有：0-1分布，二项分布，泊松分布，几何分布（首次成功模型），超几何分布。连续的有：均匀分布，指数分布，正态分布。这些都是普通密度函数中的特例而已。密度函数千奇百怪，除了那些之外，还有很难用简单的式子表示出来。在描述一般的密度函数时，通常采用密度函数估计。总而言之，关于密度函数的分类如下：
（1）参数估计
（2）半参数估计：混合模型
（3）非参数估计：直方图估计；质朴估计；核估计；k-最近邻估计
这里讲第（2）种情况。在自然界中，正态分布是一种很美的数学形式，之所以说美，就是它能成功地解释和验证了许多实际问题，绝非诗人笔下之美。在分类问题中，如果只用单纯的一个正态分布来描述，直观地讲，就有点可笑。为了说明问题，举个极端的例子，要把人和狗分类，人的身高近似为正态分布，狗的身高也近似为正态分布，但如果把两者合在一起而只想用简单的一个正态分布来描述，那误差将会很大。
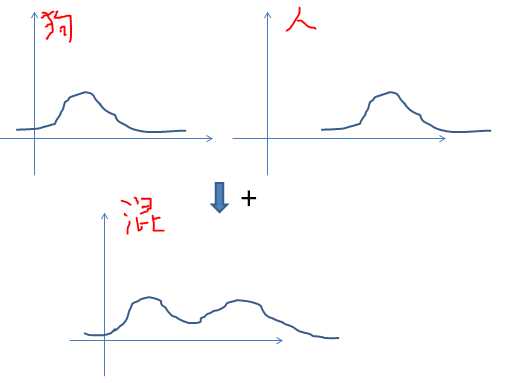
我们知道，正态分布（高斯分布）是钟形的，显然人和狗独自的分布可以近似为正态分布，但是，两者叠加之后不再是钟形的分布，用单纯的正态分布不能再描述，此时只能使用GMM模型（高斯混合模型），它的数学表达式是：
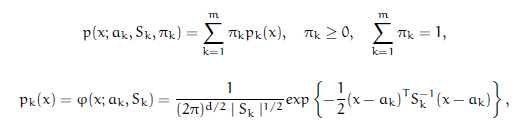
这里，就是叠加，而且
是权值，更像是条件概率，如狗占0.2，人占0.8。
二、求解模型参数
建立了混合模型，似乎一切都已经轻松愉快，只需要用下最大似然估计就可以了？好吧，思路是对的，只不过列出似然函数之后，很难求导，囧！EM算法就是解决这个尴尬的问题而准备的。这里的推导很多博客都推导过了，这里不详细地讲，只是简单列出式子：
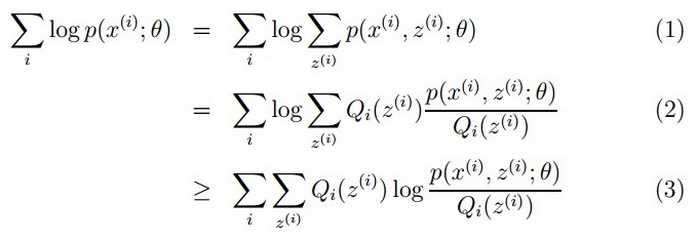
这里做的事是，不断地找对数似然函数的的下界并不断逼近该函数。当然，如果你能够想到一种方法求解最大值，速度比EM算法快，使用内存大小合理，那EM算法可以去死了。从（1）式子看来，偏导什么的不给力啊！我觉得叫它“迭代的偏导”比较合适，为啥？因为它总是先保持一个变量不变，控制另一个变量不变而是似然函数最大，接着交换过来，保持另一个变量不变，而调整这个变量，如此循环，如图：
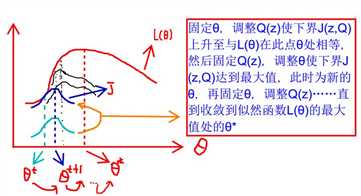
好吧，总结一下，在循环之中，可以：（1）固定θ，调整Q(z)使下界J(z,Q)上升至与L(θ)在此点θ处相等（2）固定Q(z)，调整θ是下界J(z,Q)最大值。
三、算法分析
将上述的说法重新描述一下：（1）不等式取等号（2）求最大值。这两个步骤就分别叫做E步，M步。下面分别详细说明：
（1）E步：
要詹森不等式取等号，当且仅当
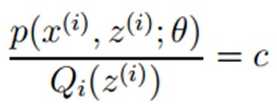
又因为
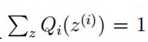
根据合比定理，c=
,再代入上上式，得
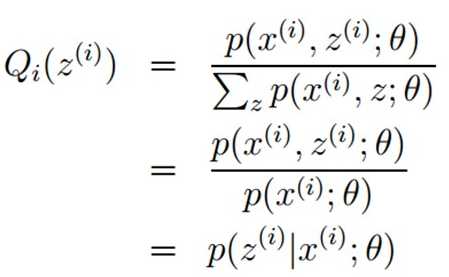
（2）求二中的（3）式最大值。
四、算法流程
五、代码构思
（1）E步骤：实际上在代码实现，会采用不化简那步
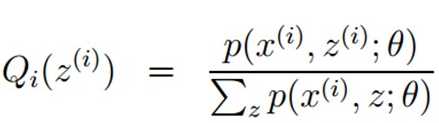
这里，联合概率密度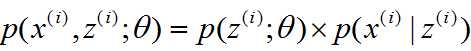
，实际上，右边第一项就是权值，第二项就是第i个正态分布.
（2）M步骤：这里求解最大值时所得到的参数值，更新参数
直接给出解析解：（表达式字母的就先不管了，粘贴一下）
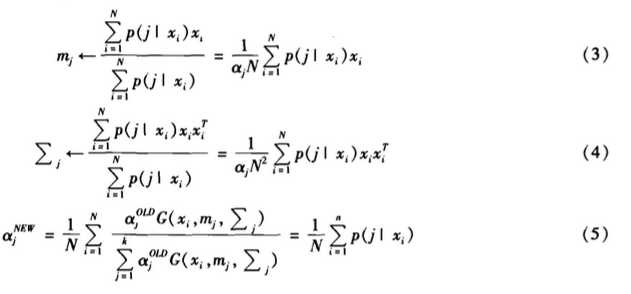
最终，根据这次的参数和上一次的参数相差大小设置一个阀值，小于这个阀值，算法终止。
六、代码
%EM M=3; % M个高斯分布混合 N=600; % 样本数 th=0.000001; % 收敛阈值 K=2; % 样本维数 % 待生成数据的参数 a_real =[2/3;1/6;1/6];%混合模型中基模型高斯密度函数的权重 mu_real=[3 4 6; 5 3 7];%均值 cov_real(:,:,1)=[5 0;0 0.2];%协方差 cov_real(:,:,2)=[0.1 0;0 0.1]; cov_real(:,:,3)=[0.1 0;0 0.1]; %生成符合标准的样本数据(每一列为一个样本) x=[ mvnrnd( mu_real(:,1) , cov_real(:,:,1) , round(N*a_real(1)) )‘ ,... mvnrnd( mu_real(:,2) , cov_real(:,:,2) , round(N*a_real(2)) )‘ ,... mvnrnd( mu_real(:,3) , cov_real(:,:,3) , round(N*a_real(3)) )‘ ]; %初始化参数 a=[1/3;1/3;1/3]; mu=[1 2 3;2 1 4]; cov(:,:,1)=[1 0;0 1]; cov(:,:,2)=[1 0;0 1]; cov(:,:,3)=[1 0;0 1]; t=inf; while t>=th a_old = a; mu_old = mu; cov_old= cov; rznk_temp=zeros(M,N); for k=1:M for n=1:N %计算P(x|mu_cm,cov_cm) rznk_temp(k,n)=exp(-1/2*(x(:,n)-mu(:,k))‘*inv(cov(:,:,k))*(x(:,n)-mu(:,k))); end rznk_temp(k,:)=rznk_temp(k,:)/sqrt(det(cov(:,:,k))); end rznk_temp=rznk_temp*(2*pi)^(-K/2); %E step %求rznk rznk=zeros(M,N); for n=1:N for k=1:M rznk(k,n)=a(k)*rznk_temp(k,n); end rznk(:,n)=rznk(:,n)/sum(rznk(:,n)); end % M step %求Nk nk=zeros(1,M); nk=sum(rznk‘); % 求a a=nk/N; % 求MU for k=1:M mu_k_sum=0; for n=1:N mu_k_sum=mu_k_sum+rznk(k,n)*x(:,n); end mu(:,k)=mu_k_sum/nk(k); end % 求COV for k=1:M cov_k_sum=0; for n=1:N cov_k_sum=cov_k_sum+rznk(k,n)*(x(:,n)-mu(:,k))*(x(:,n)-mu(:,k))‘; end cov(:,:,k)=cov_k_sum/nk(k); end %终止条件，让权值的增量，均值的增量，协方差的增量三者的范数最大者小于th(阀值) t=max([norm(a_old(:)-a(:))/norm(a_old(:));norm(mu_old(:)-mu(:))/norm(mu_old(:));norm(cov_old(:)-cov(:))/norm(cov_old(:))]); end %输出结果并比较 a_real a mu_real mu cov_real cov
参考文献：
http://blog.csdn.net/zouxy09/article/details/8537620
http://blog.sina.com.cn/s/blog_6c7b434d01013zwe.html
http://wenku.baidu.com/view/60c583294b73f242336c5fbc.html
http://baike.baidu.com/link?url=7xqVVBHCNcCy8H7FYlw_cW8hZe8ZACKsnhOVGfiO_0nz3UsJc2ermFXs5adW0w-FEoMrcFcU3C4qAh9mE9U3H_
标签：
原文地址：http://www.cnblogs.com/Wanggcong/p/4665237.html
