标签:style blog http color 使用 strong
2014.07.07 22:03
简介:
跳表(skip list)是一种随机化的有序数据结构。从形状上来看,长得比较像分层索引。能够在接近对数级别的时间内完成增、删、改、查操作。
你姑且可以认为这种数据结构的用途、用法都和平衡树很相似,但内部的实现原理则完全不同。
图示:
下面是一条有序的单链表:
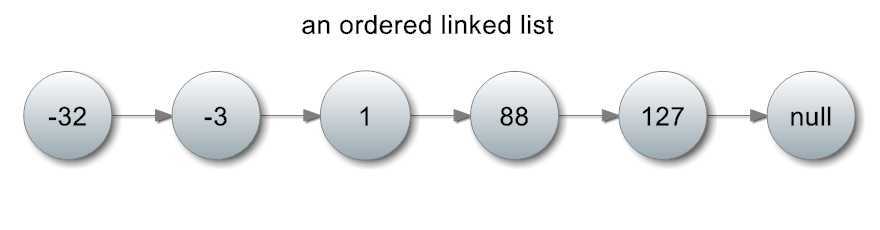
如果你要查找某一个整数,必然需要O(n)级别的时间去搜索链表。
但如果从这个链表抽取几个元素,然后在上面加上一层呢,比如这样:
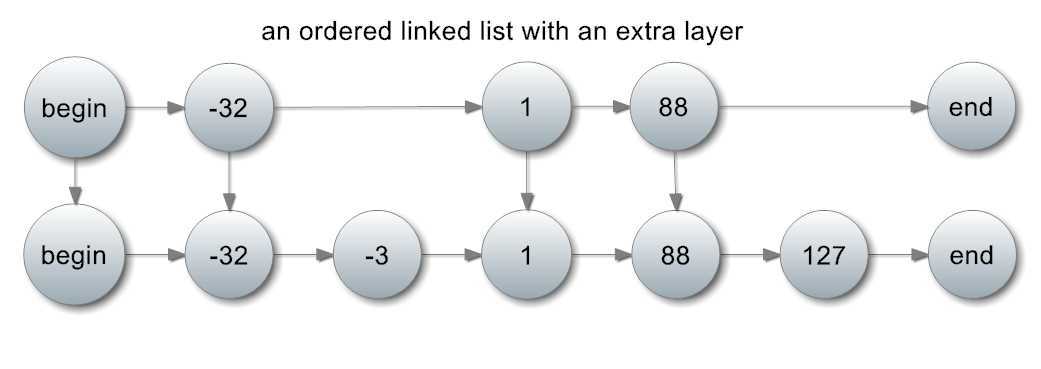
上面的双层链表的上层是通过从下层抽取一部分元素得到的。并且上下之间也存在指针链接,允许由上至下、由左至右的遍历。
这么做有什么用呢?我们先继续看看这个:
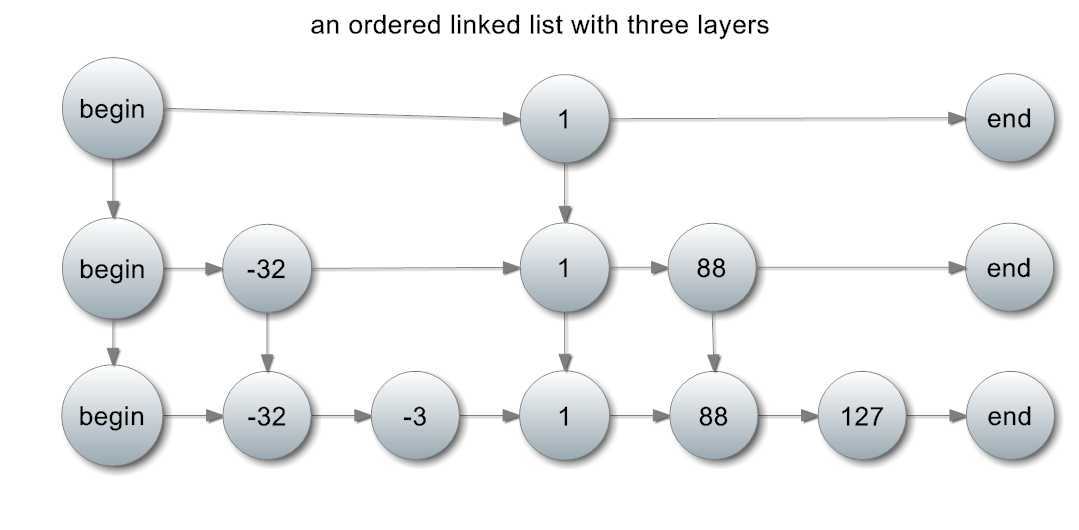
我们可以像这样,从每一层选出部分元素,在正上方组成新的一层,这样就能够形成一个看起来不整齐的多层链表。
这个图形很不规则,我们来考虑一个规则的情况:如果这个多层链表恰好有5层,每层元素个数分别为1,2,4,8,16。那么查找任意一个元素是不是能够在对数时间内完成呢?
答案当然是可以。因为多层索引的代表结构——B+树就是这种形状规则而且有序的分层结构。稳定的对数级别的操作时间就是它们的最大优势。
跳表使用另一种思维方式来构造一个类似的分层结构,但是因为包含了随机数而导致形状没那么“规则”,所以效率接近对数级别,但不稳定。
刚才我们的描述方式是一层一层地构建了这个多层链表,而正确的理解方式应该是——一个一个地插入节点。关键在于每个插入的节点有可能只插入一层,也有可能插入多层。
下面是一个空的跳表:
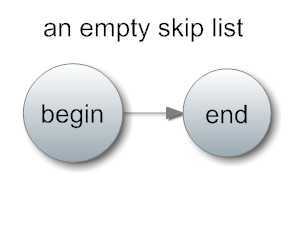
其中begin表示一个实际的节点,尽管其中的数据没有意义,我们需要它的指针进行移动。end则可以用空指针NULL来代表,表示链表尾。
下面如果我们要插入一个整数34,并且插入的高度是3层,结果将是这样:
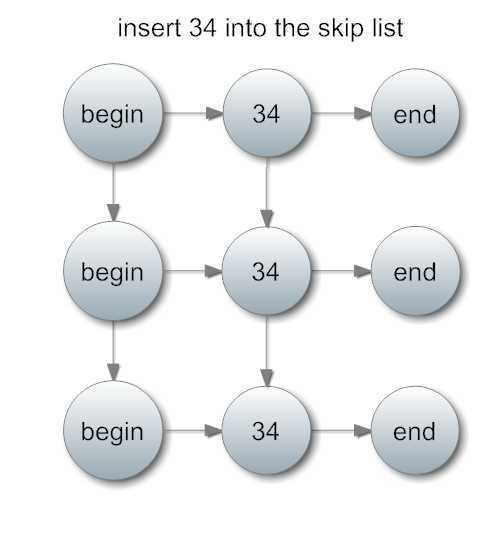
如此一来有了3个34。接下来我们再插入5,插入1层:
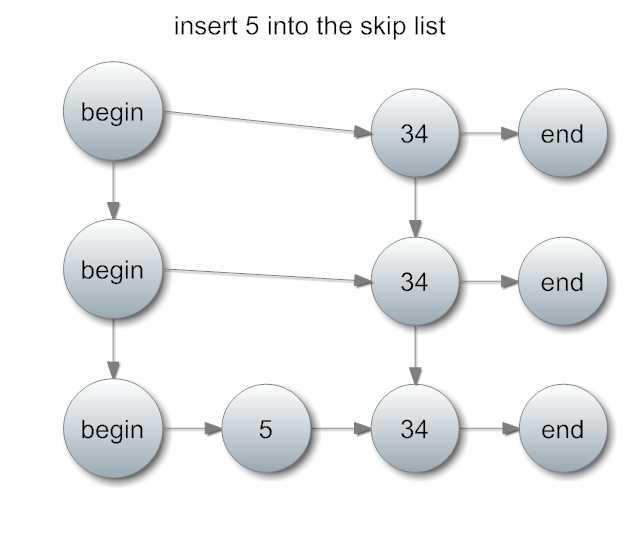
那么插入的规则是怎么定的呢?比如将元素x插入到第k层?
如果我们将最底层定义为1层,那么x元素将被插入到1~k的所有层中。
当你从跳表的左端顶部的begin节点出发时,在每一层你都只能至多向右或向下走一步。
由于每一层的链表都是有序的,所以插入元素时每一层的操作就和有序单链表的操作一样了。
于是我们从第k层开始插入,完成后下降到k-1层,逐层插入直到最底层。
下面我们再插入元素7,高度为2:
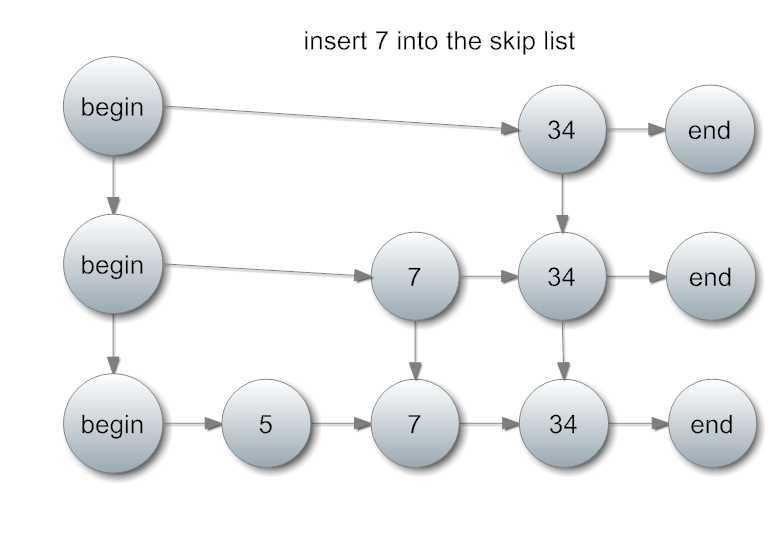
那么,每个元素插入的高度怎么决定呢?随机定就行了。此处“随机”的方法,指的是抛硬币。
如果每次有50%的概率抛出正面,那么我们就一直抛硬币,抛出正面为止,看看到底要抛多少次。将抛硬币的次数作为高度(至少抛一次,所以高度至少为1)。
这样的随机方法严格服从于p=0.5的几何分布。因此期望高度为2,虽然偶尔也能出现很高的层数。
那么,这种多层的结构并不是严格的二分查找,为何它的基本操作的效率接近对数级呢?
1. 越是在高层,移动一步就能跨过越多的元素,步子越大速度越快
2. 分析一下几何分布的分布列,此处从概率上是符合二分规律的,因此“接近对数”是有理论支持的
教材上对于跳表的评价是:一种平衡树的替代品,实现简便,效率不错。
亲自实现之后,发现跳表虽然也没那么简单,但的确比AVL树简单多了。也许我们基本不需要亲自写这些结构,但至少应该了解这种随机化的数据结构为何如此巧妙。
在我的印象里,这本书的第十章尽管充满了精华知识,在我大二的数据结构课程里,老师却几乎只字未提。
就我们学校而言,计算机教育实在是囫囵吞枣。课程好几十门,没有一门深入过。难怪我现在复习这本教材几乎等于重新学习。
呵呵的是教育,惭愧的是自己。你区区一个本科生,既然什么都不会就别拽了。赶紧学习吧。
(跳表还可以进一步优化为确定性跳表,不过那部分我已经无力研究了,饶了我吧)
实现:
1 // My implementation for skip list. 2 #include <cstdlib> 3 #include <ctime> 4 #include <iostream> 5 #include <string> 6 using namespace std; 7 8 template <class TKey> 9 struct ListNode { 10 TKey *key; 11 ListNode *down; 12 ListNode *next; 13 14 ListNode(): key(nullptr), down(nullptr), next(nullptr) {} 15 }; 16 17 template <class TKey> 18 class SkipList { 19 public: 20 SkipList() { 21 m_root = new ListNode<TKey>(); 22 m_size = 0; 23 m_level = 0; 24 } 25 26 bool contains(const TKey &key) { 27 if (m_size == 0) { 28 return false; 29 } 30 31 ListNode<TKey> *ptr = m_root; 32 while (true) { 33 if (ptr->next != nullptr) { 34 if (key < *(ptr->next->key)) { 35 if (ptr->down != nullptr) { 36 ptr = ptr->down; 37 } else { 38 return false; 39 } 40 } else if (key > *(ptr->next->key)) { 41 ptr = ptr->next; 42 } else { 43 return true; 44 } 45 } else { 46 if (ptr->down != nullptr) { 47 ptr = ptr->down; 48 } else { 49 return false; 50 } 51 } 52 } 53 } 54 55 void insert(const TKey &key) { 56 if (contains(key)) { 57 return; 58 } 59 60 ListNode<TKey> *ptr; 61 int new_level = _randomLevel(); 62 63 if (new_level > m_level) { 64 // Extra levels need to be added. 65 for (int i = m_level; i < new_level; ++i) { 66 ptr = new ListNode<TKey>(); 67 ptr->down = m_root; 68 m_root = ptr; 69 } 70 m_level = new_level; 71 } 72 73 int lvl = m_level; 74 ListNode<TKey> *last, *cur; 75 76 ptr = m_root; 77 last = cur = nullptr; 78 while (true) { 79 if (ptr->next != nullptr) { 80 if (key < *(ptr->next->key)) { 81 if (lvl <= new_level) { 82 cur = new ListNode<TKey>(); 83 if (last == nullptr) { 84 cur->key = new TKey(key); 85 } else { 86 cur->key = last->key; 87 last->down = cur; 88 } 89 last = cur; 90 cur->next = ptr->next; 91 ptr->next = cur; 92 } 93 94 if (ptr->down != nullptr) { 95 ptr = ptr->down; 96 --lvl; 97 } else { 98 break; 99 } 100 } else if (key > *(ptr->next->key)) { 101 ptr = ptr->next; 102 } else { 103 break; 104 } 105 } else { 106 if (lvl <= new_level) { 107 cur = new ListNode<TKey>(); 108 if (last == nullptr) { 109 cur->key = new TKey(key); 110 } else { 111 cur->key = last->key; 112 last->down = cur; 113 } 114 last = cur; 115 cur->next = ptr->next; 116 ptr->next = cur; 117 } 118 119 if (ptr->down != nullptr) { 120 ptr = ptr->down; 121 --lvl; 122 } else { 123 break; 124 } 125 } 126 } 127 ++m_size; 128 } 129 130 void erase(const TKey &key) { 131 if (!contains(key)) { 132 return; 133 } 134 135 ListNode<TKey> *ptr = m_root; 136 ListNode<TKey> *cur; 137 while (true) { 138 if (ptr->next != nullptr) { 139 if (key < *(ptr->next->key)) { 140 if (ptr->down != nullptr) { 141 ptr = ptr->down; 142 } else { 143 break; 144 } 145 } else if (key > *(ptr->next->key)) { 146 ptr = ptr->next; 147 } else { 148 cur = ptr->next; 149 ptr->next = cur->next; 150 if (ptr->down != nullptr) { 151 delete cur; 152 ptr = ptr->down; 153 } else { 154 delete cur->key; 155 delete cur; 156 break; 157 } 158 } 159 } else { 160 if (ptr->down != nullptr) { 161 ptr = ptr->down; 162 } else { 163 break; 164 } 165 } 166 } 167 --m_size; 168 169 ptr = m_root; 170 while (ptr->next == nullptr) { 171 // Empty levels are removed. 172 if (ptr->down == nullptr) { 173 break; 174 } else { 175 m_root = m_root->down; 176 delete ptr; 177 ptr = m_root; 178 --m_level; 179 } 180 } 181 } 182 183 size_t size() { 184 return m_size; 185 } 186 187 void clear() { 188 _clearUp(); 189 190 m_root = new ListNode<TKey>(); 191 m_size = 0; 192 m_level = 0; 193 } 194 195 void debugPrint() { 196 ListNode<TKey> *p1, *p2; 197 198 cout << ‘{‘ << endl; 199 p1 = m_root; 200 while (p1 != nullptr) { 201 p2 = p1->next; 202 cout << " "; 203 while (p2 != nullptr) { 204 cout << *(p2->key) << ‘ ‘; 205 p2 = p2->next; 206 } 207 cout << endl; 208 p1 = p1->down; 209 } 210 cout << ‘}‘ << endl; 211 } 212 213 ~SkipList() { 214 _clearUp(); 215 } 216 private: 217 int m_level; 218 int m_size; 219 ListNode<TKey> *m_root; 220 221 void _clearUp() { 222 ListNode<TKey> *head = m_root; 223 ListNode<TKey> *p1, *p2; 224 225 while (head != nullptr) { 226 p1 = head; 227 head = head->down; 228 while (p1 != nullptr) { 229 p2 = p1->next; 230 if (p1->key != nullptr && p1->down == nullptr) { 231 delete p1->key; 232 } 233 delete p1; 234 p1 = p2; 235 } 236 } 237 } 238 239 int _randomLevel() { 240 int level = 0; 241 242 while (rand() & 1) { 243 ++level; 244 } 245 246 return level; 247 } 248 }; 249 250 int main() 251 { 252 srand((unsigned int)time(nullptr)); 253 string s; 254 SkipList<int> sl; 255 int key; 256 257 while (cin >> s) { 258 if (s == "i") { 259 cin >> key; 260 sl.insert(key); 261 } else if (s == "c") { 262 cin >> key; 263 cout << (sl.contains(key) ? "Yes" : "No") << endl; 264 } else if (s == "e") { 265 cin >> key; 266 sl.erase(key); 267 } else if (s == "cl") { 268 sl.clear(); 269 } 270 sl.debugPrint(); 271 } 272 sl.clear(); 273 274 return 0; 275 }
《数据结构与算法分析:C语言描述》复习——第十章“算法设计技巧”——跳表,布布扣,bubuko.com
《数据结构与算法分析:C语言描述》复习——第十章“算法设计技巧”——跳表
标签:style blog http color 使用 strong
原文地址:http://www.cnblogs.com/zhuli19901106/p/3830665.html