堆排序

标签：

堆

如下图所示。（二叉堆）是一个数组，它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。

A.length给出数组元素的个数，A.heap-size表示有多少个堆元素存储在该数组中。

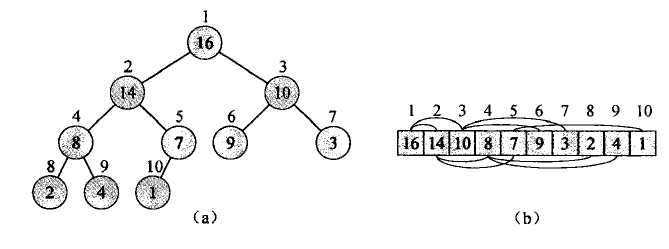
树的根结点是A[1]，这样给定一个结点的下标i，我们很容易计算得到它的父结点、左孩子和右孩子的下标

PARENT(i)
return i/2        //向下取整

LEFT(i)
return 2i

RIGHT(i)
return 2i+1

二叉堆可以分为两种形式：最大堆和最小堆。在这两种堆中，结点的值都要满足堆的性质

在最大堆中，最大堆性质是指出来根以外的所有结点i都要满足：

A[PARENT(i)]>=A[i]

也就是说，某个结点的值之多与其父结点一样大。因此，堆中的最大元素存放在根结点中。而最小堆性质刚好相反。

在堆排序算法中，我们使用的是最大堆。最小堆通常用于构造优先队列。

维护堆的性质

MAX-HEAPIFY是用于维护最大堆性质的重要过程。

它的输入为一个数组A和一个下标i。在调用MAX-HEAPIFY的时候，我们假定根结点为LEFT(i)和RIGHT(i)的二叉树是最大堆。

这时A[i]有可能小于其孩子，违背了最大堆的性质。MAX-HEAPIFY通过让A[i]的值在最大堆中“逐级下降”，从而使得以下标i为根结点的子树重新遵循最大堆性质。

MAX-HEAPIFY(A,i)
l=LEFT(i)
r=RIGHT(i)
if l<=A.heap-size and A[l]>A[i]
    largest=l
else
    largest=i
if r<=A.heap-size and A[r]>A[largest]
    largest=r
if largest!=i
    exchange A[i] with A[largest]
    MAX-HEAPIFY(A,largest) 

下面是执行MAX-HEAPIFY(A,2)的情况

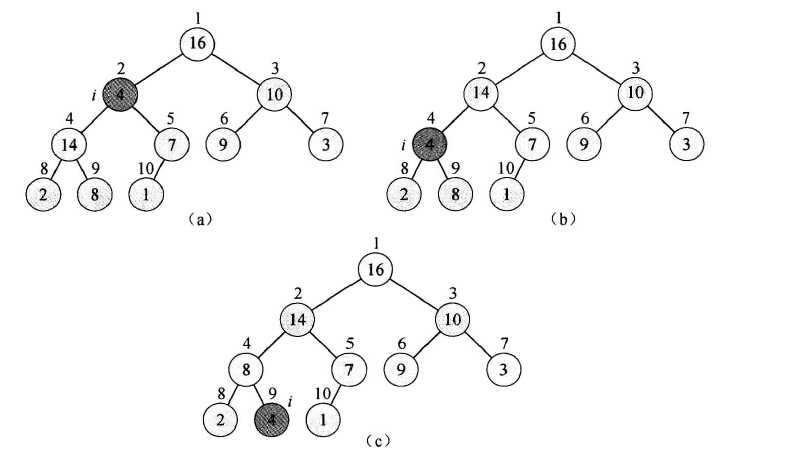
在程序的每一步，从A[i],A[LEFT(i)]和A[RIGHT[i]]中选出最大的，并将其下标存储在largest中。

如果A[i]是最大的，那么以i为结点的子树已经是最大堆，程序结束。否则，最大元素是i的某个孩子结点，则交换A[i]和A[largest]的值。

交换之后，下标为largest的结点的值是原来的A[i]，以该节点为根的子树又可能违反最大堆性质。因此，需要对该子树递归调用MAX-HEAPIFY。

对于一个树高为h的结点来说，MAX-HEAPIFY的时间复杂度是O(h)

建堆

我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n=A.length的数组转换成最大堆。

子数组A(n/2+1...n)中的元素都是树的叶结点，每个叶结点都可以看成包含一个元素的堆，所以只需要对树中的其它结点调用一次MAX-HEAPIFY

BUILD-MAX-HEAP(A)
A.heap-size=A.length
for i=A.length/1 downto 1
    MAX-HEAPIFY(A,i) 

堆排序算法

初始时候，堆排序算法利用BUILD-MAX-HEAP将输入数组A[1...n]建成最大堆。

因为数组中的最大元素总在根结点A[1]中，通过把它与A[n]进行交换（把A[1]放到数组最后），我们可以让该元素放在正确的位置。

这时候，我们从堆中去掉结点n(通过减少A.heap-size的值来实现)，原来跟的孩子结点仍然是最大最，而新的根结点可能会违背最大堆性质，因此我们需要调用MAX-HEAPIFY(A,1)在A[1...n-1]上构造一个新的最大堆。

堆排序算法会不断重复这一过程，直到堆的大小从n-1降到2

HEAPSORT(A)
BUILD-MAX-HEAP(A)
for i=A.length downto 2
    exchange A[1] with A[i]
    A.heap-size=A.heap-size-1
    MAX-HEAPIFY(A,1) 

实现与测试代码

 1 #include <iostream>
 2 #include <algorithm>
 3 using namespace std;
 4 
 5 int heap_size;
 6 
 7 void max_heapify(int arr[],int i)
 8 {
 9     int l=2*i;
10     int r=2*i+1;
11     int largest;
12     if(l<=heap_size&&arr[l]>arr[i])
13         largest=l;
14     else
15         largest=i;
16     if(r<=heap_size&&arr[r]>arr[largest])
17         largest=r;
18     if(largest!=i)
19     {
20         swap(arr[i],arr[largest]);
21         max_heapify(arr,largest);
22     }    
23 }
24 
25 void build_max_heap(int arr[],int length)
26 {
27     heap_size=length;
28     for(int i=length/2;i>=1;--i)
29         max_heapify(arr,i);
30 } 
31 
32 void heapsort(int arr[],int length)
33 {
34     build_max_heap(arr,length);
35     for(int i=length;i>=2;--i)
36     {
37         swap(arr[1],arr[i]);
38         heap_size--;
39         max_heapify(arr,1);
40     }
41 }
42 
43 int main()
44 {
45     int arr[]={0,4,1,3,2,16,9,10,14,8,7};
46     heapsort(arr,10);
47     for(int i=1;i<=10;++i)
48         cout<<arr[i]<<‘ ‘;
49     cout<<endl;
50     system("pause");
51 }

View Code

堆排序

标签：

原文地址：http://www.cnblogs.com/runnyu/p/4677170.html