标签:
0 K-means算法简介
K-means是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一。
K-means算法的基本思想是:以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。

public static Map<Integer, List<Integer>> kMeans(List<List<Double>> dataSet, int k, List<List<Double>> centerPointCp) { /** * 拷贝中心点,防止修改原始数据 */ List<List<Double>> centerPoint = new ArrayList<List<Double>>(); for(int i = 0; i < centerPointCp.size(); i++){ List<Double> tmpCp = new ArrayList<Double>(); for(int j = 0; j < centerPointCp.get(i).size(); j++){ tmpCp.add(centerPointCp.get(i).get(j)); } centerPoint.add(tmpCp); } int n = dataSet.size(); int dim = dataSet.get(0).size(); double[][] clusterAssment = new double[n][2]; Boolean clusterChanged = true; while (clusterChanged) { clusterChanged = false; for (int i = 0; i < n; i++) { double minDist = Double.POSITIVE_INFINITY; int minIndex = -1; for (int j = 0; j < k; j++) { double distIC = PreData.distance(dataSet.get(i), centerPoint.get(j)); if (distIC < minDist) { minDist = distIC; minIndex = j; } } if (clusterAssment[i][0] != minIndex) { clusterChanged = true; } clusterAssment[i][0] = minIndex; clusterAssment[i][1] = Math.pow(minDist, 2); } for (int i = 0; i < k; i++) { double[] tmp = new double[dim]; int cnt = 0; for (int j = 0; j < n; j++) { if (i == clusterAssment[j][0]) { for (int m = 0; m < dim; m++) { tmp[m] += dataSet.get(j).get(m); } cnt += 1; } } if (cnt != 0) { for (int m = 0; m < dim; m++) { centerPoint.get(i).set(m, tmp[m] / cnt); } } } } //List<List<Double>> Map<Integer, List<Integer>> ret = new TreeMap<Integer, List<Integer>>(); for(int i = 0; i < n; i++){ for(int j = 0; j < k; j++){ if(clusterAssment[i][0] == j){ if(ret.containsKey(j)){ ret.get(j).add(i); }else{ List<Integer> tmp = new ArrayList<Integer>(); tmp.add(i); ret.put(j, tmp); } break; } } } return ret; }
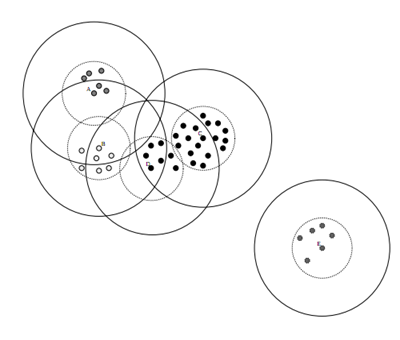

public static int canpoy(List<List<Double>> dataSet, double T1, double T2) { List<List<List<Double>>> canP = new ArrayList<List<List<Double>>>(); Random rand = new Random(); while (dataSet.size() > 0) { int randNum = rand.nextInt(dataSet.size()); List<List<Double>> tmpCanp = new ArrayList<List<Double>>(); tmpCanp.add(dataSet.get(randNum)); canP.add(tmpCanp); dataSet.remove(randNum); for (int i = 0; i < dataSet.size();) { Boolean flag = false; for (int j = 0; j < canP.size(); j++) { if (distance(dataSet.get(i), canP.get(j).get(0)) < T1) { //遍历canp, 小于T1,加入canp,可以重复加入 canP.get(j).add(dataSet.get(i)); if (distance(dataSet.get(i), canP.get(j).get(0)) < T2) { //如果小于T2, 则移除该点 flag = true; } } } if (flag) { dataSet.remove(i); // } else { i++; //注意list的remove的特点 } } } return canP.size(); }
若只考虑计算K值,可省略上面T1,改变后的代码如下

public static int canpoy(List<List<Double>> dataSet, double T2) { List<List<List<Double>>> canP = new ArrayList<List<List<Double>>>(); Random rand = new Random(); while (dataSet.size() > 0) { int randNum = rand.nextInt(dataSet.size()); List<List<Double>> tmpCanp = new ArrayList<List<Double>>(); tmpCanp.add(dataSet.get(randNum)); canP.add(tmpCanp); dataSet.remove(randNum); for (int i = 0; i < dataSet.size();) { Boolean flag = false; for (int j = 0; j < canP.size(); j++) { if (PreData.distance(dataSet.get(i), canP.get(j).get(0)) < T2) { flag = true; } } if (flag) { dataSet.remove(i); } else { i++; } } } return canP.size(); }
上面初始canpoy的选择依赖于随机数,结果也会变化。为了得到稳定的K值,可以多做几次测试,取出现次数最多的值。
阈值T2采用所有数的距离平均值代替。测试次数取30-100次即可。代码如下

import java.util.ArrayList; import java.util.List; import java.util.Map; import java.util.Random; import java.util.TreeMap; public class ClusterNum { /** * 计算阈值T2,用来计算聚类个数 * * @param testData * @return */ public static double averageT(List<List<Double>> testData) { double ret = 0; int cnt = 0; for (int i = 0; i < testData.size(); i++) { for (int j = i + 1; j < testData.size(); j++) { ret += PreData.distance(testData.get(i), testData.get(j)); cnt++; } } return ret / cnt; } /** * canpoy算法寻找聚类簇的数量 * * @param dataSet * @param T1 * @param T2 * @return */ public static int canpoy(List<List<Double>> dataSet, double T2) { List<List<List<Double>>> canP = new ArrayList<List<List<Double>>>(); Random rand = new Random(); while (dataSet.size() > 0) { int randNum = rand.nextInt(dataSet.size()); List<List<Double>> tmpCanp = new ArrayList<List<Double>>(); tmpCanp.add(dataSet.get(randNum)); canP.add(tmpCanp); dataSet.remove(randNum); for (int i = 0; i < dataSet.size();) { Boolean flag = false; for (int j = 0; j < canP.size(); j++) { if (PreData.distance(dataSet.get(i), canP.get(j).get(0)) < T2) { flag = true; } } if (flag) { dataSet.remove(i); } else { i++; } } } return canP.size(); } /** * 得到聚类个数 * @param data * @param testNum 检验次数,建议设置范围30-100 * @return */ public static int getClusterNum(List<List<Double>> data, int testNum) { int i = 0; Map<Integer, Integer> bop = new TreeMap<Integer, Integer>(); while (i < testNum) { List<List<Double>> dataCopy = new ArrayList<List<Double>>(); dataCopy.addAll(data); double T2 = averageT(dataCopy); int k = canpoy(dataCopy, T2); if (bop.containsKey(k)) { bop.put(k, bop.get(k) + 1); } else { bop.put(k, 1); } i++; } int tmp = 0, index = 0; for (Integer key : bop.keySet()) { if (bop.get(key) > tmp) { tmp = bop.get(key); index = key; } } return index; } }

import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; public class ClusterCenter { /** * 计算密度参数MinPts * * @param beta * @param sampleSize * @return */ public static int getMinPts(double beta, int sampleSize) { int ret = (int) (beta * sampleSize / Math.sqrt(sampleSize)); return ret; } /** * 计算得到半径 * * @param data * @param theta * @return */ public static double getRadius(List<List<Double>> data, double theta) { int n = data.size(); double disSum = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { disSum += PreData.distance(data.get(i), data.get(j)); } } return theta * disSum / Math.pow(n, 2); } /** * 得到高密度点集合 * * @param data * @param MinPts * @param radius * @return */ public static Map<List<Double>, Integer> getHighDensitySet ( List<List<Double>> data, int MinPts, double radius, int k) throws RuntimeException{ Map<List<Double>, Integer> ret = new HashMap<List<Double>, Integer>(); int n = data.size(); for (int i = 0; i < n; i++) { int cnt = 0; for (int j = 0; j < n; j++) { if (i != j) { double tmp = PreData.distance(data.get(i), data.get(j)); if (tmp < radius) { cnt++; } } } if (cnt >= MinPts) { ret.put(data.get(i), cnt); } } if (ret.size() < k) { throw new RuntimeException("参数错误,请减小beta值或增大theta值!"); } return ret; } /** * 得到初始中心 * * @param k * @param highDensitySet * @return */ public static List<List<Double>> getInitCenter(int k, Map<List<Double>, Integer> highDensitySet) { List<List<Double>> ret = new ArrayList<List<Double>>(); List<Double> tmp = null; double maxValue = 0; for (List<Double> key : highDensitySet.keySet()) { if (maxValue < highDensitySet.get(key)) { maxValue = highDensitySet.get(key); tmp = key; } } ret.add(tmp); highDensitySet.remove(tmp); maxValue = 0; for (List<Double> key : highDensitySet.keySet()) { if (maxValue < PreData.distance(tmp, key)) { maxValue = PreData.distance(tmp, key); tmp = key; } } ret.add(tmp); highDensitySet.remove(tmp); int cnt = 2; while (cnt < k) { maxValue = 0; tmp = null; double rs = 1; for (List<Double> key : highDensitySet.keySet()) { for (int i = 0; i < ret.size(); i++) { rs *= PreData.distance(key, ret.get(i)); } if (maxValue < rs) { maxValue = rs; tmp = key; } } ret.add(tmp); highDensitySet.remove(tmp); cnt++; } return ret; } }
3 熊忠阳, 陈若田,张玉芳 《一种有效的k-means聚类中心初始化方法》 重庆大学 http://pan.baidu.com/s/1dD2Mr9B
标签:
原文地址:http://www.cnblogs.com/hdu-2010/p/4682185.html