标签:
本文的主要内容来自《Functional Programming in Swift》这本书,有点所谓的观后总结
在本书的Introduction章中:
we will try to focus on some of the qualities that we believe well-designed functional programs in Swift should exhibit:
1. Modulatity【模块化】
2. A Careful Treatment of Mutable State 【细心对待可变的状态】: 不变性和无副作用
3.Types【类型】
其实上面的3点在我上篇文章已经详细介绍了。
Thinking Functionally ----- 函数式编程思想,这是本书的第二章
Functions in Swift are first-class values
下面我们根据书中的例子来阐述下本章的主要内容:
1. The first function we write, inRange1, checks that a point is in the grey。核查一个point是否在某个范围内,相对于(0,0)
判断目标点到原点的距离是不是<= range
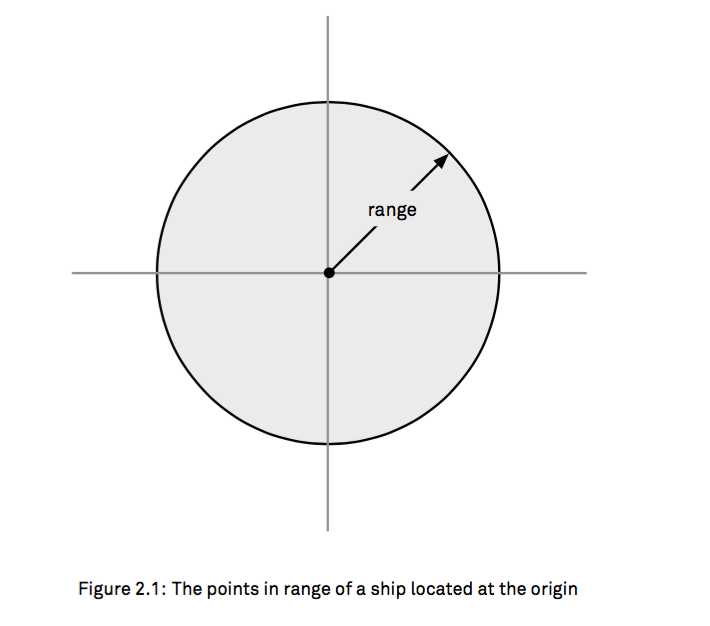
typealias Position = CGPoint
typealias Distance = CGFloat func inRange1(target: Position, range: Distance) -> Bool { return sqrt(target.x * target.x + target.y * target.y) <= range }
2. We now add an argument representing the location of the ship to our inRange function:
inRange方法中增加一个代表船的位置的参数:
判断两个点之间的距离是不是<= range
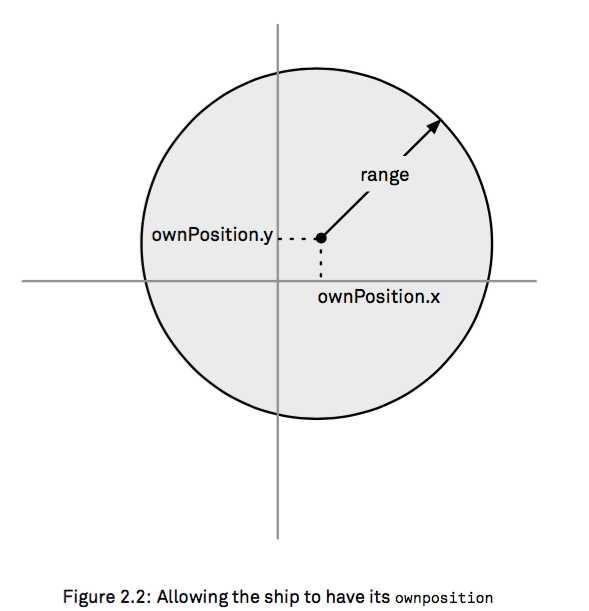
func inRange2(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(dx * dx + dy * dy)
return targetDistance <= range
}
现在你意识到如果target 理你太近了你要躲避它。这个时候我们定义一个minimumDistance 来代表安全距离
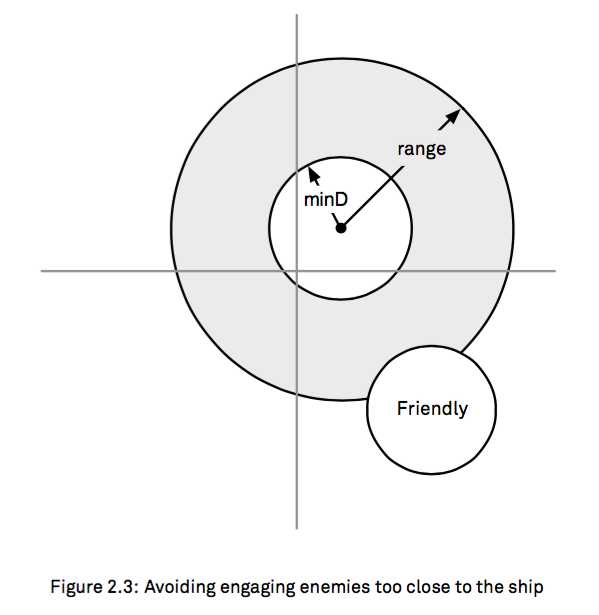
let minimumDistance: Distance = 2.0
func inRange3(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(dx * dx + dy * dy)
return targetDistance <= range && targetDistance >= minimumDistance
}
最后,你也需要去逃离 其他的离你比较近的ships。
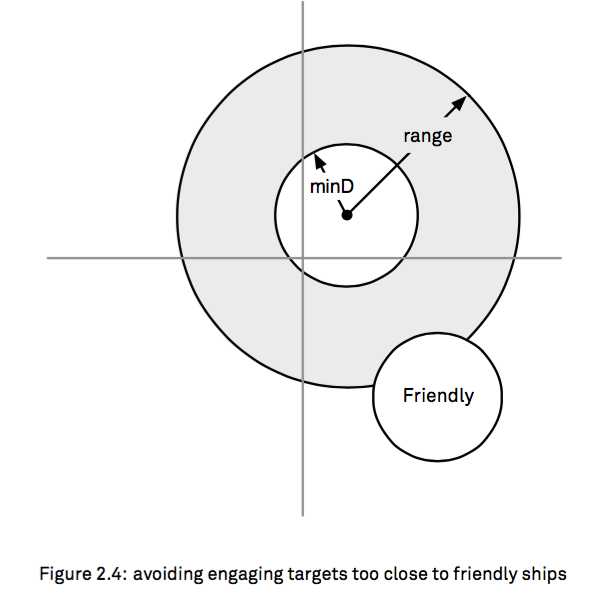
func inRange4(target: Position, ownPosition: Position, friendly: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(dx * dx + dy * dy)
let friendlyDx = friendly.x - target.x
let friendlyDy = friendly.y - target.y
let friendlyDistance = sqrt(friendlyDx * friendlyDx + friendlyDy * friendlyDy)
return targetDistance <= range
&& targetDistance >= minimumDistance
&& (friendlyDistance >= minimumDistance)
}
swift之函数式编程(二)------- Thinking Functionally
标签:
原文地址:http://www.cnblogs.com/Ohero/p/4685592.html