标签:
描述
南将军统率着N个士兵,士兵分别编号为1~N,南将军经常爱拿某一段编号内杀敌数最高的人与杀敌数最低的人进行比较,计算出两个人的杀敌数差值,用这种方法一方面能鼓舞杀敌数高的人,另一方面也算是批评杀敌数低的人,起到了很好的效果。
所以,南将军经常问军师小工第i号士兵到第j号士兵中,杀敌数最高的人与杀敌数最低的人之间军功差值是多少。
现在,请你写一个程序,帮小工回答南将军每次的询问吧。
注意,南将军可能询问很多次。
输入
只有一组测试数据
第一行是两个整数N,Q,其中N表示士兵的总数。Q表示南将军询问的次数。(1<N<=100000,1<Q<=1000000)
随后的一行有N个整数Vi(0<=Vi<100000000),分别表示每个人的杀敌数。
再之后的Q行,每行有两个正正数m,n,表示南将军询问的是第m号士兵到第n号士兵。输出
对于每次询问,输出第m号士兵到第n号士兵之间所有士兵杀敌数的最大值与最小值的差。
样例输入
5 2
1 2 6 9 3
1 2
2 4
样例输出
1
裸的RMQ问题,这个题我们用ST算法
ST算法是在线算法,用动态规划的思想预处理输入数据,之后立刻回答每一次询问,整个算法非常高效,预处理祭出O(nlogn)的复杂度,而询问只需要O(1)的复杂度。
首先我们解决预处理的部分:(这里我们假定询问的是最大值)
1 for(int j=1;j<=m;j++) 2 { 3 for(int i=1;i<=n;i++) 4 { 5 if(i+(1<<(j-1))<=n) maxx[i][j]=max(maxx[i][j-1],maxx[i+(1<<(j-1))][j-1]); 6 } 7 }
其实根据状态的定义我们就明白了,递推的顺序是自底向上的,必须以小区间的值来更新大区间的值,而且必须较小区间全部处理完整,才能继续处理较大区间,如果嵌套相反了,那么结果必然是错误的。
而其中m的值,就是2的多少次幂的计算,是用log2n来计算出的。
----------------------------------------我只是一条分割线-------------------------------------------------
那么我们继续分析算法的查询部分,上面的预处理似乎都无法把区间给询问囊括进去,或者说都超过了询问的区间,该怎么解决呢?
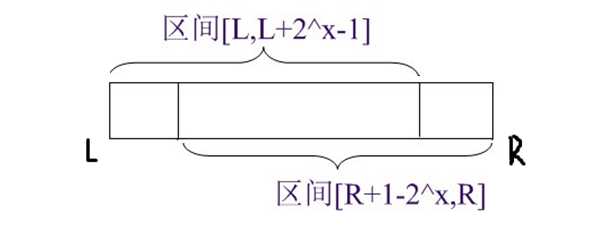
想必看到图就懂了23333。我们要做的只是把x的值计算出来,图中可得2x<=r-l+1,那么最大的x=log2(r-l+1)
到这里算法的分析部分结束,直接贴代码。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 #include<algorithm> 6 #include<iostream> 7 using namespace std; 8 const int maxn=100000+10; 9 int n,q; 10 int a[maxn],maxx[maxn][20],minn[maxn][20]; 11 void init() 12 { 13 for(int i=1;i<=n;i++) maxx[i][0]=minn[i][0]=a[i]; 14 int m=(int)(log(n*1.0)/log(2.0)); 15 for(int j=1;j<=m;j++) 16 { 17 for(int i=1;i<=n;i++) 18 { 19 if(i+(1<<(j-1))<=n) maxx[i][j]=max(maxx[i][j-1],maxx[i+(1<<(j-1))][j-1]); 20 if(i+(1<<(j-1))<=n) minn[i][j]=min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]); 21 } 22 } 23 } 24 int rmqmin(int l,int r) 25 { 26 int m=(int)(log(r-l+1)*1.0/log(2.0)); 27 return min(minn[l][m],minn[r-(1<<m)+1][m]); 28 } 29 int rmqmax(int l,int r) 30 { 31 int m=(int)(log(r-l+1)*1.0/log(2.0)); 32 return max(maxx[l][m],maxx[r-(1<<m)+1][m]); 33 } 34 void read() 35 { 36 cin>>n>>q; 37 for(int i=1;i<=n;i++) 38 { 39 scanf("%d",&a[i]); 40 } 41 init(); 42 } 43 void work() 44 { 45 int l,r; 46 for(int i=1;i<=q;i++) 47 { 48 scanf("%d%d",&l,&r); 49 int x1=rmqmax(l,r); 50 int x2=rmqmin(l,r); 51 printf("%d\n",x1-x2); 52 } 53 } 54 int main() 55 { 56 read(); 57 work(); 58 return 0; 59 }
标签:
原文地址:http://www.cnblogs.com/sajuuk/p/4686660.html