标签:
这道题搜了一晚上的题解,外加自己想了半个早上,终于想得很透彻了。于是打算好好写一写这题题解,而且这种做法比网上大多数题解要简单而且代码也比较简洁。
首先要把题读懂,把输入读懂,这实际上是一颗有向树。第i(2≤i≤n)行的两个数u,d,其中u是i的父亲结点,d是距离。
第一遍DFS我们可以计算出以u为根的子树中,距离u最远的结点的距离d(u, 0)以及次远的距离d(u, 1)。而且,这两个不在u的同一棵子树中,如果u只有一个孩子,那么d(u, 1) = 0
第一遍DFS完以后,因为1是整棵树的跟,所以d(1, 0)就是距离1最远的距离。然后第二遍DFS,这次是用根的信息来更新它的子节点,此时d(u,0)d(u,1)的含义变为整棵树中距u最长和次长的距离。
如图:
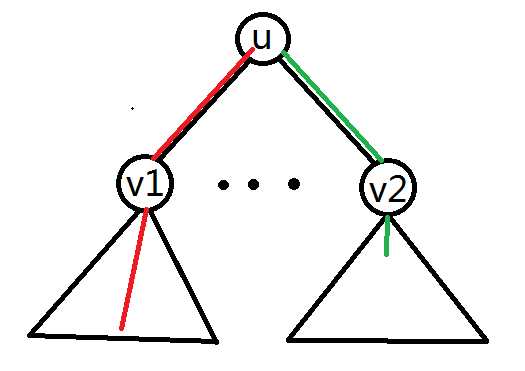
红线代表距u最长的距离,绿线是次长。因为最长距离在v1的子树中,所以就用dis(u, v1) + d(u, 1)(也就是那条绿线)来更新距v1的最长和次长距离; 用dis(u, v2) + d(u, 0)(那条红线)来更新距v2的最长次长距离。
因此最终答案就是d(u, 0)

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <vector> 5 using namespace std; 6 7 const int maxn = 10000 + 10; 8 vector<int> G[maxn], C[maxn]; 9 int n; 10 11 int d[maxn][2]; 12 13 void dfs(int u) 14 { 15 for(int i = 0; i < G[u].size(); i++) 16 { 17 int v = G[u][i]; 18 dfs(v); 19 int t = d[v][0] + C[u][i]; 20 if(t > d[u][0]) swap(t, d[u][0]); 21 if(t > d[u][1]) swap(t, d[u][1]); 22 } 23 } 24 25 void dfs2(int u) 26 { 27 for(int i = 0; i < G[u].size(); i++) 28 { 29 int v = G[u][i], t, w = C[u][i]; 30 if(d[v][0] + w == d[u][0]) t = w + d[u][1]; 31 else t = w + d[u][0]; 32 if(t > d[v][0]) swap(t, d[v][0]); 33 if(t > d[v][1]) swap(t, d[v][1]); 34 dfs2(v); 35 } 36 } 37 38 int main() 39 { 40 scanf("%d", &n); 41 for(int u = 2; u <= n; u++) 42 { 43 int v, d; scanf("%d%d", &v, &d); 44 G[v].push_back(u); C[v].push_back(d); 45 } 46 47 dfs(1); 48 dfs2(1); 49 50 for(int i = 1; i <= n; i++) printf("%d\n", d[i][0]); 51 52 return 0; 53 }
标签:
原文地址:http://www.cnblogs.com/AOQNRMGYXLMV/p/4691522.html