标签:
本文参考自《复杂性思考》一书的第二章,并给出这一章节里我的习题解答。
(这书不到120页纸,要卖50块!!,一开始以为很厚的样子,拿回来一看,尼玛。。。。。代码很少,给点提示,然后让读者自己思考怎么实现)
先定义顶点和边
1 class Vertex(object): 2 def __init__(self, label=‘‘): 3 self.label = label 4 def __repr__(self): 5 return ‘Vertex(%s)‘ % repr(self.label) 6 # __repr__返回表达式, __str__返回可阅读信息 7 __str__=__repr__ # 使其指向同一个函数 8 9 class Edge(tuple): 10 # 继承自建tuple类型并重写new方法 11 def __new__(cls, e1, e2): 12 return tuple.__new__(cls, (e1,e2)) 13 def __repr__(self): 14 return "Edge(%s, %s)" % (repr(self[0]), repr(self[1])) 15 __str__ = __repr__
创建顶点和编的方法如下
if __name__=="__main__": # 创建两个顶点一条边 v = Vertex(‘v‘) w = Vertex(‘w‘) e = Edge(v,w) # print e # 将顶点和边放入图中 g = Graph([v,w],[e]) # print g
创建一个基本的图类:
1 # 通过字典的字典实现图的结构 2 class Graph(dict): 3 def __init__(self, vs=[], es=[]): 4 """ 建立一个新的图,(vs)为顶点vertices列表,(es)为边缘edges列表 """ 5 for v in vs: 6 self.add_vertex(v) 7 for e in es: 8 self.add_edge(e) 9 10 def add_vertex(self,v): 11 """ 添加顶点 v: 使用字典结构""" 12 self[v] = {} 13 14 def add_edge(self, e): 15 """ 添加边缘 e: e 为一个元组(v,w) 16 在两个顶点 w 和 v 之间添加成员e ,如果两个顶点之间已有边缘,则替换之 """ 17 v, w = e 18 # 由于一条边会产生两个项目,因此该实现代表了一个无向图 19 self[v][w] = e 20 self[w][v] = e
# 练习2-2解答:图的一些基本操作
1 def get_edge(self,v1, v2): 2 """ 接收两个顶点,若这两个顶点之间右边则返回这条边,否则返回None """ 3 try: 4 return self[v1][v2] 5 except: 6 return None 7 8 def remove_edge(self,e): 9 """ 接受一条边,并且删除图中该边的所有引用 """ 10 v, w = e 11 self[v].pop(w) 12 self[w].pop(v) 13 14 def vertices(self): 15 """ 返回图中所有顶点的列表 """ 16 return self.keys() 17 18 def edges(self): 19 """ 返回图中边的列表 """ 20 es = set() # 为了避免返回重复的边,设为集合 21 for v1 in self.vertices(): 22 for v2 in self.vertices(): 23 es.add(self.get_edge(v2, v1)) 24 es.discard(None) # 若集合中存在None元素,则删除 25 return list(es) 26 """ 利用图的字典结构获得所有边 27 es = [] 28 for v in self.vertices(): 29 es.extend(self[v].values()) 30 es = list(set(es)) 31 return es 32 """ 33 34 def out_vertices(self,v): 35 """ 接受一个Vertex并返回邻近顶点(通过一条边连接到给定节点的节点)的列表 """ 36 return self[v].keys() 37 38 def out_edges(self,v): 39 """ 接受一个Vertex并返回连接到给定节点的边的列表 """ 40 return self[v].values() 41 42 def add_all_edges(self,vs=None): 43 """ 从一个无边的图开始,通过在各个顶点间添加边来生成一个完全图 44 输入为目标顶点的列表,如果为None,则对所有的点进行全联结 """ 45 if vs == None: 46 vs = self.vertices() 47 for v1 in vs: 48 for v2 in vs: 49 if v1 is v2 : continue # 假设不存在单顶点连通 50 self.add_edge(Edge(v1,v2))
习题2-3 生成正则图
正则图是指图中每个顶点的度相同,生成正则图需要顶点数和度数满足一定条件,具体算法见注释:
1 def add_regular_edges(self,k): 2 """ 从一个无边的图开始不断添加边,使得每个顶点都有相同的度k 3 一个节点的度指的是连接到它的边的数量 """ 4 n = len(self.vertices()) 5 assert n > 1 6 if k==1: 7 vs = self.vertices() 8 for i in range(n-1): 9 self.add_edge(Edge(vs[i],vs[i+1])) 10 return True 11 if n < k+1: 12 print "Cannot create regular graph" 13 return False 14 if n == k+1: 15 self.add_all_edges() 16 return True 17 """ 18 设度数为k,图的阶数(顶点个数)为n 19 利用归纳方法生成边的个数 20 偶数度 当k=2m,m>=1时 21 递归过程: 22 0. 假设n>k+1,因为当n=k+1时,只要生成全连接即可,当n<k+1,则不能生成正则图 23 1. 当n>k+1时:先从原图中前k+1个顶点(v1,v2,...,v2m-1,v2m, v2m+1)生成完全图 24 此时,该k+1个顶点的度数均为k 25 2. 现添加一个顶点vx,x=2m+2该顶点的度为0 26 3. 删除m条不相连的边,如(v1,v2),(v3,v4),(v5,v6),...,(v2m-1,v2m),这时顶点v1,v2,...v2m的度为k-1 27 记录下这m条边的顶点 28 4. 联结 (v1,vx),(v2,vx),...,(v2m-1,vx),(v2m,vx),使得v1,v2,...,v2m,v2m+2的度=k 29 5. 对新加入的点,重复3,4 30 31 奇数度 当k=2m+1,m>=1时 32 递归过程: 33 设图G是有n个顶点的k正则图,且k=2m+1,m>=1,按照下面法则生成新图G1 34 0. 假设n>k+1,因为当n=k+1时,只要生成全连接即可,当n<k+1,则不能生成正则图 35 1. 在图G中任取m条顶点不同的边(x1,x2),(x3,x4),(x5,x6),...,(x2m-1,x2m) 记为组es1 36 再另取m条顶点不同的边 (y1,y2),(y3,y4),(y5,y6),...,(y2m-1,y2m) 记为组es2 37 其中xi和yj可以存在相同,但是两组中的所有边都不相同 38 此时,该k+1个顶点的度数均为k 39 2. 在图G中去掉m条边(x1,x2),(x3,x4),(x5,x6),...,(x2m-1,x2m),增加新的顶点v1,并增加2m条新边 40 (v1,x1),(v1,x2),...,(v1,x2m-1),(v1,x2m) 41 3. 在图G中去掉m条边(y1,y2),(y3,y4),(y5,y6),...,(y2m-1,y2m),增加新的顶点v2,并增加2m条新边 42 (v2,y1),(v2,y2),...,(v2,y2m-1),(v2,y2m) 43 4. 增加新边 (v1,v2) 44 5. 对新的点v3,v4,重复1,2,3,4 45 增加的顶点和边保证了v1,v2和x1,x2,...,x2m,y1,y2,...,y2m的度数为2m+1其余顶点度数不变 46 """ 47 if k%2==0: 48 # 选取前k+1个点,先构造完全图 49 vs = self.vertices() 50 self.add_all_edges(vs[:k+1]) 51 for i in range(k+1,n): # 对之后的点进行遍历 52 vsdel = [] # 记录删除过边的顶点 53 for e in self.edges(): 54 # 获得边的两个顶点 55 v1,v2 = e[0],e[1] 56 if v1 not in vsdel and v2 not in vsdel: 57 vsdel.append(v1) 58 vsdel.append(v2) 59 # 删除不相连的边 60 self.remove_edge(e) 61 # 当已删除的边数为k/2,即共k个非邻近点时,退出循环 62 if len(vsdel)==k: 63 break 64 # 将新的点与记录的点进行连接 65 for v in vsdel: 66 self.add_edge(Edge(v,vs[i])) 67 else: 68 if n%2==0 and n>k+1: # 由上述法则可知,n必须为偶数 69 # 选取前k+1个偶数点,先构造完全图 70 vs = self.vertices() 71 self.add_all_edges(vs[:k+1]) 72 73 for i in range(k+1,n,2): # 之后的点进行两两遍历 74 vsdel1 = [] # 记录第1组删除的点 75 edel1 = [] # 记录第1组删除的边 76 for e in self.edges(): 77 # 获得边的两个顶点 78 v1,v2 = e[0],e[1] 79 if v1 not in vsdel1 and v2 not in vsdel1: 80 vsdel1.append(v1) 81 vsdel1.append(v2) 82 # 删除不相连的边 83 edel1.append(e) 84 self.remove_edge(e) 85 # 当已删除的边数为m,即共k-1个非邻近点时,退出循环 86 if len(vsdel1)==k-1: 87 break 88 89 vsdel2 = [] # 记录第2组删除的点 90 edel2 = [] # 记录第2组删除的边 91 for e in self.edges(): 92 # 获得边的两个顶点 93 v1,v2 = e[0],e[1] 94 # 点可以和第一组相同,但边不可以 95 if v1 not in vsdel2 and v2 not in vsdel2 and e not in edel1: 96 vsdel2.append(v1) 97 vsdel2.append(v2) 98 # 删除不相连的边 99 edel2.append(e) 100 self.remove_edge(e) 101 # 当已删除的边数为m,即共k-1个非邻近点时,退出循环 102 if len(vsdel2)==k-1: 103 break 104 105 # 分别连接两组边 106 for v in vsdel1: 107 self.add_edge(Edge(v,vs[i])) 108 for v in vsdel2: 109 self.add_edge(Edge(v,vs[i+1])) 110 self.add_edge(Edge(vs[i],vs[i+1])) 111 else: 112 print "Cannot create regular graph" 113 return False 114 return True
习题2-4:判断一个图是否连通,可以用BFS实现:
1 def is_connect(self): 2 """ 判断一个图是否连通的 3 从任意顶点开始进行一次BFS,将所有到达的节点都标记上,然后检查是否所有的节点都被标记上 """ 4 pass 5 vs = self.vertices() # 获得所有顶点 6 7 q, s = [], set() # 搜索队列,标记集合 8 q.append(vs[0]) # 从第1个顶点开始搜索 9 while q: # 当队列非空 10 v = q.pop(0) # 从队列中删除移一个顶点 11 s.add(v) # 并标记当前顶点 12 # 搜索当前顶点的连接点,如果这些连接点没有被标记 13 # 则将其添加到队列中 14 for w in self.out_vertices(v): 15 if w not in s: 16 q.append(w) 17 # 当队列为空时完成搜索,检查标记过的顶点是否等于图的顶点数 18 if len(s)==len(vs): 19 return True 20 else: 21 return False
测试代码:需要用到作者书中网页提供的GraphWorld.py实现可视化功能
1 from GraphWorld import CircleLayout,GraphWorld 2 from Graph import Graph,Vertex,Edge 3 import string 4 5 6 def test(n,k): 7 # create n Vertices 8 labels = string.ascii_lowercase + string.ascii_uppercase 9 vs = [Vertex(c) for c in labels[:n]] 10 11 # create a graph and a layout 12 g = Graph(vs) 13 g.add_regular_edges(k) 14 layout = CircleLayout(g) 15 16 # draw the graph 17 gw = GraphWorld() 18 gw.show_graph(g, layout) 19 gw.mainloop() 20 21 22 if __name__ == ‘__main__‘: 23 test(n=10,k=3)
以下为生成10个结点,度为3的正则图:
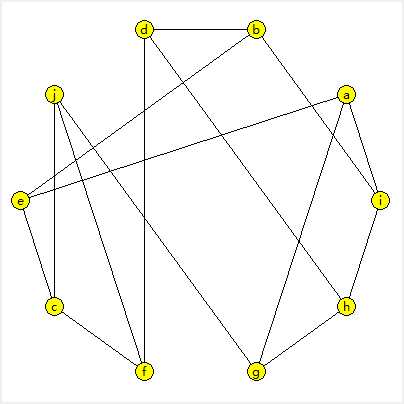
生成随机图,继承上面的Graph类:
1 from Graph import Graph,Vertex,Edge 2 from random import randint 3 4 5 class RandomGraph(Graph): 6 """ 随即图 """ 7 def add_random_edges(self,p): 8 """ 从一个·无边图开始随机生成边 9 使得任意两个节点间存在边的概率为p (0<=p<=1) """ 10 for v1 in self.vertices(): 11 for v2 in self.vertices(): 12 if v1 is v2: continue 13 if randint(0,100) < p*100 : 14 self.add_edge(Edge(v1,v2)) 15
测试一下:
1 from GraphWorld import CircleLayout,GraphWorld 2 import string 3 4 def test(n,p): 5 # create n Vertices 6 labels = string.ascii_lowercase + string.ascii_uppercase 7 vs = [Vertex(c) for c in labels[:n]] 8 9 # create a graph and a layout 10 g = RandomGraph(vs) 11 g.add_random_edges(p) 12 print "connect?:",g.is_connect() 13 layout = CircleLayout(g) 14 15 # draw the graph 16 gw = GraphWorld() 17 gw.show_graph(g, layout) 18 gw.mainloop() 19 20 21 if __name__ == ‘__main__‘: 22 test(p=0.2,n=5) 23
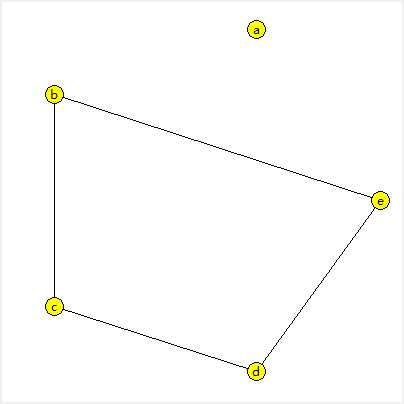
迭代器部分代码:
1 # 迭代器 2 class AllTrue(object): 3 def next(self): 4 return True 5 def __iter__(self): 6 return self 7 8 # 使用AllTrue之类的迭代器可以表现无限序列 9 print zip(‘abc‘,AllTrue()) 10 11 # 通过编写生成器函数创建一个迭代器 12 def generate_letters(): 13 for letter in ‘abc‘: 14 yield letter 15 16 iter = generate_letters() 17 18 import string 19 # 带有无限循环的生成器会返回一个不会终止的迭代器 20 def alphabet_cycle(): 21 while True: 22 for i in range(1,10): 23 for c in string.lowercase: 24 yield c+str(i) 25 26 iter_ac = alphabet_cycle() 27 print iter_ac.next()
标签:
原文地址:http://www.cnblogs.com/hanahimi/p/4693260.html