标签:
1、优化模型的两种策略:
1)基于残差的方法
残差其实就是真实值和预测值之间的差值,在学习的过程中,首先学习一颗回归树,然后将“真实值-预测值”得到残差,再把残差作为一个学习目标,学习下一棵回归树,依次类推,直到残差小于某个接近0的阀值或回归树数目达到某一阀值。其核心思想是每轮通过拟合残差来降低损失函数。
总的来说,第一棵树是正常的,之后所有的树的决策全是由残差来决定。
2)使用梯度下降算法减小损失函数。
对于一般损失函数,为了使其取得最小值,通过梯度下降算法,每次朝着损失函数的负梯度方向逐步移动,最终使得损失函数极小的方法(此方法要求损失函数可导)。
2、GB(Gradient Boosting)梯度提升算法
GB其实是一个算法框架,即可以将已有的分类或回归算法放入其中,得到一个性能很强大的算法。
GB总共需要进行M次迭代,每次迭代产生一个模型,我们需要让每次迭代生成的模型对训练集的损失函数最小,而如何让损失函数越来越小呢?我们采用梯度下降的方法,在每次迭代时通过向损失函数的负梯度方向移动来使得损失函数越来越小,这样我们就可以得到越来越精确的模型。
梯度提升算法(GB)过程如下:[1]
1)初始化损失函数。
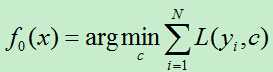
2)对于第m轮迭代,当m<=M时循环执行A)~D) (m=1,2,…,M)
A)计算残差rmi:
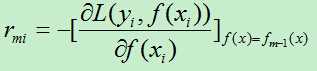
计算损失函数的负梯度在当前模型的值,将它作为残差的估计,对于平方损失函数它就是残差,对于一般损失函数,它就是残差的近似值。
B)对rmi拟合一颗回归树,得到第m课树的叶节点区域Rmj。(j=1,2,…,J)
(估计回归树叶节点区域,拟合残差近似值)
C)对j=1,2,…,J,线性搜索出损失函数的最小值
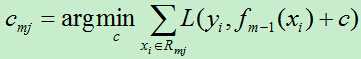
D)更新f(x)
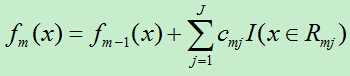
3)得到回归树
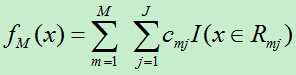
下面给出Friedman大牛论文中的GB算法[6],论文下载链接:http://pan.baidu.com/s/1pJxc1ZH

图2.1 Gradient Boost算法[6]
3、GBDT (Gradient Boosting Decision Tree):梯度提升决策树算法
此处主要讨论多类Logistic回归问题

图3.1 多类logistic回归算法[6]
关于以上代码,网友已有分析:[5] (在此借用)
“1. 表示建立M棵决策树(迭代M次)
2. 表示对函数估计值F(x)进行Logistic变换
3. 表示对于K个分类进行下面的操作(其实这个for循环也可以理解为向量的操作,每一个样本点xi都对应了K种可能的分类yi,所以yi, F(xi), p(xi)都是一个K维的向量,这样或许容易理解一点)
4. 表示求得残差减少的梯度方向
5. 表示根据每一个样本点x,与其残差减少的梯度方向,得到一棵由J个叶子节点组成的决策树
6. 为当决策树建立完成后,通过这个公式,可以得到每一个叶子节点的增益(这个增益在预测的时候用的)
每个增益的组成其实也是一个K维的向量,表示如果在决策树预测的过程中,如果某一个样本点掉入了这个叶子节点,则其对应的K个分类的值是多少。
7. 的意思为,将当前得到的决策树与之前的那些决策树合并起来,作为新的一个模型
”
最后本人对GBDT研究得还不够透彻,下次研究清楚了再专门写一篇GBDT的文章!!
参考文献:
[1] 李航,统计学习方法。
[2] 林轩田,机器学习技法。
[3] 程序员之家,http://www.programerhome.com/?p=3665
[4] DianaCody, http://www.dianacody.com/2014/11/01/GBRT.html
[5] leftnoteasy, http://www.cnblogs.com/leftnoteasy/archive/2011/03/07/random-forest-and-gbdt.html
[6] Friedman J H. Greedy Function Approximation: A Gradient Boosting Machine[C]// Annals of Statistics1999:1189--1232.
标签:
原文地址:http://www.cnblogs.com/liuwu265/p/4694191.html