标签:
要理解深度优先搜索必须理解递归的本质,递归的核心思想在于在一个函数还没有执行完成的时候就调用自身,这样就会形成一个树状的结构,从而使其可以一直延伸下去,进而覆盖所有可能的分支。直到某一层递归条件满足,才开始收敛。

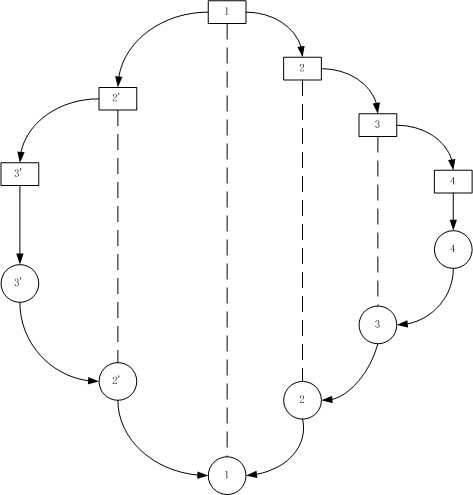
Figure 1 递归
Note:图中序号相同而且用虚线相连接的一个方块和圆圈对表示一次函数调用
从图中可以看出递归具有很强的可回退性和选择性,图中的2和2’是一次递归的不同分支,3和3’是一次递归的不同分支。函数执行到某一层次之后完全可以选择任何一个分支进行收敛,这点刚好符合深度优先搜索的需求。
宽度优先搜索算法,其本质则是基于树状结构,每到一层,先把该层所有的未遍历的节点添加到队列,再判断每一个节点是否满足条件,如果满足退出即可,否则,再到下一层继续遍历。
在遍历的过程中每一层的遍历都在上一层遍历的后面,这一点正是队列的特点——先把一个节点对应的下一层可达的节点全部添加到队列尾,继续遍历上一层的队列,上一层结束后遍历下一层的节点。
这两种搜索算法都能够生成所有能够遍历到的状态,因而在需要对所有状态进行处理时使用宽度优先搜索算法时是可以的。但是使用递归函数则实现比较简单一点,而且状态的管理也更简单。故而一般还是使用深度优先搜索算法实现。但是在求最短路径的时候一般还是使用宽度优先搜索算法。
宽度优先搜索算法一般会把状态逐个添加到队列中,也就是说内存与状态数成正比,而深度优先搜索算法则是与最大递归数成正比,所以一般认为深度优先搜索算法更为节省内存。
标签:
原文地址:http://www.cnblogs.com/tianyou/p/4695452.html