扩展欧几里得算法

标签：

　　对于 a 、b 不全为0，存在整数 x 和 y 使得 gcd(a,b)=x*a+y*b ; 整数。。。也就是可以使负的。

     代码：

 1 int exGcd(int a,int b,int &x,int &y)
 2 {
 3   if(b==0)
 4   {
 5     x=1;
 6     y=0;
 7     return a;
 8   }
 9   int r=exGcd(b,a%b,x,y);
10   int t=x;
11   x=y;
12   y=t-a/b*y;
13   return r;
14 }

扩展欧几里得算法

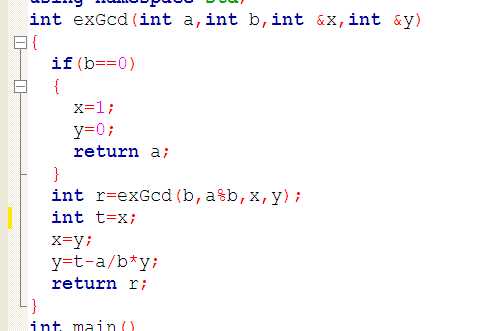
　　首先，我们看一下他是怎么形成的。从最后一层往上推：首先b=0 时得到最大公约数 a ，return a; 现在看上一层，从r那句后继续往下运行，可以知道，此后，每次都从r 句 获得已经得到的最大公约数，然后再往下执行。。。

     对于倒二层的a、b来说,b就是a、b的最大公约数，那么有 b = x1*a + y1*b ; （即 x1=0; y1=1;） 

　  同样，对于倒三层的a、b来说，倒二层的b也是这一层a、b的最大公约数 有 b‘ =  x2*a + y2*b ; b‘=a%b;  b‘=x1*a‘+y1*b‘ ;   b‘=x1*b+y1*(a%b) ;

---> x1*b+y1*(a%b) = x2*a+ y2*b;

 ---->   (***) 这一步非常关键。就是化解a%b  x1*b+y1*(a-a/b*b) = x2*a + y2*b (这里的除是计算机编程里的除)

----->  合并同类项   x1*b + a* y1 - (a/b*b)*y1= x2*a+y2*b;

----> b*(x1-a/b*y1)+a*y1=x2*a+y2*b;

----->   x2=y1; y2=x1- a/b *y1;  (la-la-la 终于出来了、、)    

　   也就是说下一层的x等于上一层的y，下一层的y等于上一层的x-a/b*上一层的y，这里的a/b是这一层的。。。这里虽然拿特列：倒二倒三层解释，但由于没有涉及具体的x、y值，所以得出的公式应该是通用的。 这解释了我们代码的写法原因，同时由倒二层可知 x1=0; y1=1; 

　　采用递归写法先到底层，然后由底层的x、y逐步上推，得到顶层的x、y，就是我们想求的x、y。。。

　　......

扩展欧几里得算法

标签：

原文地址：http://www.cnblogs.com/hchlqlz-oj-mrj/p/4706272.html