标签：
原来一听到网络最大流啊，什么BFS，DFS的就感觉特别的陌生，也感觉特别的头疼，如今我终于要学习到这里了这也标志着我要真正的要学习算法和搞acm了，所以我更要努力的学习力求向上把它学好。
不废话了，这最大流问题通过我今天的学习和理解终于有点眉目了，我就做个随笔，首先了解一下容量网络，百度了一下：
容量网络：在有向图D=（V，A），指定一个点为发点，记作
，指定另一个点为收点，记作
，其余点叫作中间点。对于A的每条弧（
），都对应一个权数
≥0，称为弧（ ）的容量，将这样的赋权有向图叫作一个容量网络，记作D=（V,A,C）。
这有点不好懂，我解释一下网络最大流的意思是，从s（源点）到t（汇点）需要通过n条路径也有可能有一条s和t直接相连的，每一条路径能通过的最大流量（容量网络）又不尽相同，我们要求的是从s到t的最大流量，如图：
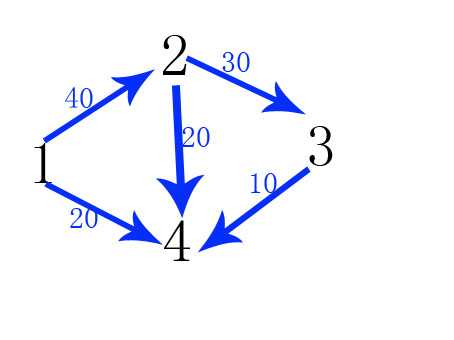
从1到4的路径有：(1)1—>4;(2)1—>2—>4;(3)1-->2-->3-->4
（1）的最大流量显然是20；（2）的最大流量是20;（3）的最大流量是10；
因为20+10+10（三条路径最大流量）<20+40（从1出发的最大流量）；所以根据此图可以找到1到4的最大流为20+10+10=50；
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <queue>
using namespace std;
const int MAX=1000000;
int map[20][20],flow[20],pre[20],n,m;
bool vis[20];
int BFS()
{
int up;
queue<int> q;
vis[1]=1;
memset(pre,-1,sizeof(pre));
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
flow[i]=MAX;
q.push(1);
while(!q.empty())
{
up=q.front();
q.pop();
if(up==n)
break;
for(int i=1;i<=n;i++)
{
if(!vis[i]&&map[up][i]>0)
{
vis[i]=1;
flow[i]=min(flow[up],map[up][i]);
pre[i]=up;
q.push(i);
}
}
}
if(!vis[n]||n==1)
return -1;
return flow[n];
}
int EK()
{
int d,maxflow=0,up,down;
maxflow=0;
while((d=BFS())!=-1)
{
maxflow+=d;
down=n;
while(down!=1)
{
up=pre[down];
map[up][down]-=d;
map[down][up]+=d;
down=up;
}
}
return maxflow;
}
int main()
{
int T,a,b,c,h=1,i;
scanf("%d",&T);
while(T--)
{
memset(map,0,sizeof(map));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&c);
map[a][b]+=c;
}
printf("Case %d: %d\n",h++,EK());
}
return 0;
}
标签：
原文地址：http://www.cnblogs.com/yuanbo123/p/4711349.html
