标签:
c4.5算法是机器学习算法中的一种分类决策树算法,其核心算法是ID3 。c4.5对ID3算法做了相对的改进。如下
1 采用信息增益率代替信息增益。因为使用信息增益时会偏向选取取值更多的属性。
2 在树的构造过程中进行剪枝
3 能够完成对连续属性的离散化处理
4 对不完整数据进行处理
c4.5算法有如下优点:产生的分类规则易于理解,准确率高。
缺点:在构造树的过程中,需要对数据集进行多次的顺序和排序,因而导致算法的低效
熵:
变量的不确定性越大,熵也就越大。熵是对信息的量化,不确定性越大,熵也就越大。因此在分类决策树中,可以选择熵最小的属性来作为分类特征。
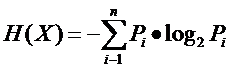
信息增益:
按名称来理解的话,就是前后信息的差值,在决策树分类问题中,即就是决策树在进行属性选择划分前和划分后的信息差值,即可以写成:
gain()=infobeforeSplit()–infoafterSplit() 即 分割前的熵减去分割后的熵
举例如下
| Outlook | Temperature | Humidity | Windy | Play? |
| sunny | hot | high | false | no |
| sunny | hot | high | true | no |
| overcast | hot | high | false | yes |
| rain | mild | high | false | yes |
| rain | cool | normal | false | yes |
| rain | cool | normal | true | no |
| overcast | cool | normal | true | yes |
| sunny | mild | high | false | no |
| sunny | cool | normal | false | yes |
| rain | mild | normal | false | yes |
| sunny | mild | normal | true | yes |
| overcast | mild | high | true | yes |
| overcast | hot | normal | false | yes |
| rain | mild | high | true | no |
上面的训练集有4个属性,即属性集合A={OUTLOOK, TEMPERATURE, HUMIDITY, WINDY};而类标签有2个,即类标签集合C={Yes, No},分别表示适合户外运动和不适合户外运动,其实是一个二分类问题。
我们已经计算过信息增益,这里直接列出来,如下所示:
数据集D包含14个训练样本,其中属于类别“Yes”的有9个,属于类别“No”的有5个,则计算其信息熵:
1 |
Info(D) = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940 |
下面对属性集中每个属性分别计算信息熵,如下所示:
1 |
Info(OUTLOOK) = 5/14 * [- 2/5 * log2(2/5) – 3/5 * log2(3/5)] + 4/14 * [ - 4/4 * log2(4/4) - 0/4 * log2(0/4)] + 5/14 * [ - 3/5 * log2(3/5) – 2/5 * log2(2/5)] = 0.694 |
2 |
Info(TEMPERATURE) = 4/14 * [- 2/4 * log2(2/4) – 2/4 * log2(2/4)] + 6/14 * [ - 4/6 * log2(4/6) - 2/6 * log2(2/6)] + 4/14 * [ - 3/4 * log2(3/4) – 1/4 * log2(1/4)] = 0.911 |
3 |
Info(HUMIDITY) = 7/14 * [- 3/7 * log2(3/7) – 4/7 * log2(4/7)] + 7/14 * [ - 6/7 * log2(6/7) - 1/7 * log2(1/7)] = 0.789 |
4 |
Info(WINDY) = 6/14 * [- 3/6 * log2(3/6) – 3/6 * log2(3/6)] + 8/14 * [ - 6/8 * log2(6/8) - 2/8 * log2(2/8)] = 0.892 |
根据上面的数据,我们可以计算选择第一个根结点所依赖的信息增益值,计算如下所示:
1 |
Gain(OUTLOOK) = Info(D) - Info(OUTLOOK) = 0.940 - 0.694 = 0.246 |
2 |
Gain(TEMPERATURE) = Info(D) - Info(TEMPERATURE) = 0.940 - 0.911 = 0.029 |
3 |
Gain(HUMIDITY) = Info(D) - Info(HUMIDITY) = 0.940 - 0.789 = 0.151 |
4 |
Gain(WINDY) = Info(D) - Info(WINDY) = 0.940 - 0.892 = 0.048 |
接下来,我们计算分裂信息度量H(V):
属性OUTLOOK有3个取值,其中Sunny有5个样本、Rainy有5个样本、Overcast有4个样本,则
1 |
H(OUTLOOK) = - 5/14 * log2(5/14) - 5/14 * log2(5/14) - 4/14 * log2(4/14) = 1.577406282852345 |
属性TEMPERATURE有3个取值,其中Hot有4个样本、Mild有6个样本、Cool有4个样本,则
1 |
H(TEMPERATURE) = - 4/14 * log2(4/14) - 6/14 * log2(6/14) - 4/14 * log2(4/14) = 1.5566567074628228 |
属性HUMIDITY有2个取值,其中Normal有7个样本、High有7个样本,则
1 |
H(HUMIDITY) = - 7/14 * log2(7/14) - 7/14 * log2(7/14) = 1.0 |
属性WINDY有2个取值,其中True有6个样本、False有8个样本,则
1 |
H(WINDY) = - 6/14 * log2(6/14) - 8/14 * log2(8/14) = 0.9852281360342516 |
根据上面计算结果,我们可以计算信息增益率,如下所示:
1 |
IGR(OUTLOOK) = Info(OUTLOOK) / H(OUTLOOK) = 0.246/1.577406282852345 = 0.15595221261270145 |
2 |
IGR(TEMPERATURE) = Info(TEMPERATURE) / H(TEMPERATURE) = 0.029 / 1.5566567074628228 = 0.018629669509642094 |
3 |
IGR(HUMIDITY) = Info(HUMIDITY) / H(HUMIDITY) = 0.151/1.0 = 0.151 |
4 |
IGR(WINDY) = Info(WINDY) / H(WINDY) = 0.048/0.9852281360342516 = 0.0487196804926 |
标签:
原文地址:http://www.cnblogs.com/lotorless/p/4712714.html