标签:
有向图中,连通性比较好理解,如果两个顶点V和顶点W是可达的,可以称之为强连通的,即存在路径A→B,同时也存在一条有向路径B→A.从之前的有向环的判定过程中其实我们可以得到一个结论就是两个是强连通的当且仅当它们都在一个普通的有向环中。强连通将所有的顶点分为了不同的集合,每个集合都是由相互均为强连通性的顶点的最大子集组成的,我们将这些集合称之为强连通分量。
一般来说技术服务于生活,如果将我们看到网页作为顶点,页面指向另外一个页面的超链接作为边,可以将数量庞大的网页分为不同的大小进行处理,作为软件工程师或者说码农,经常遇到的就是模块的封装,如果将模块作为顶点,模块之间的引用作为边,通过强连通图我们可以更好进行模块之间的调用关系考虑适时的解耦。如果通过平方级别的算法解决强连通分量,那么遇到大型有向图的过程我们就会有点力不从心。Kosaraju的算法(也称为Kosaraju-Sharir算法)是线性时间的算法来解决有向图中的连通性查询以及处理强连通分量的数量。
采用之前有向环中的图片:
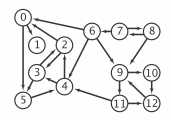
API定义:
@interface KosarajuCC : NSObject //记录顶点是否被标记 @property (strong,nonatomic) NSMutableArray *marked; @property (assign,nonatomic) NSInteger count;//连通的分量 @property (strong,nonatomic) NSMutableArray *ids;//顶点所在的连通分量的标识符 //连通分量递归初始化 -(instancetype)initWithGraph:(Digraph *)graph; -(void)depthSearch:(Digraph *)graph vertex:(NSInteger)vertex; //判断两个顶点之间是否存在连通性 -(BOOL)stronglyConnected:(NSInteger)vertex otherVertex:(NSInteger)otherVertex; @end
通过API的定义,如果对比之前之前无向图中的API,我们发现基本上没有变化,具体实现的过程中变化也很小,需要之前基于深度优先搜索的顶点排序,取出逆后序集合进行遍历即可,之后和无向图中一样进行递归判断存储在数组中。
@implementation KosarajuCC
#pragma mark getter and setter
-(NSMutableArray *)marked{
if (!_marked) {
_marked=[[NSMutableArray alloc]initWithCapacity:1];
}
return _marked;
}
-(NSMutableArray *)ids{
if (!_ids) {
_ids=[[NSMutableArray alloc]initWithCapacity:1];
}
return _ids;
}
-(instancetype)initWithGraph:(Digraph *)graph{
self=[super init];
if (self) {
for (NSInteger i=0; i<graph.vertexs;i++) {
[self.marked addObject:[NSNull null]];
[self.ids addObject:[NSNull null]];
}
DepthFirstOrder *order=[[DepthFirstOrder alloc]initWithGraph:[graph reverse]];
//遍历图的顶点
for (NSInteger j=0; j<[order.reversePostStack count]; j++) {
NSInteger temp=[[order.reversePostStack objectAtIndex:j] integerValue];
if (![self isMarked:temp]) {
[self depthSearch:graph vertex:temp];
self.count++;
}
}
}
return self;
}
//博客园-FlyElephant:http://www.cnblogs.com/xiaofeixiang/
-(void)depthSearch:(Digraph *)graph vertex:(NSInteger)vertex{
self.marked[vertex]=[NSNumber numberWithBool:true];
//同一分量中顶点的赋值
self.ids[vertex]=[NSNumber numberWithInteger:self.count];
for (NSInteger i=0; i<[graph.adjDataSource[vertex] count]; i++) {
NSInteger temp=[[graph.adjDataSource[vertex] objectAtIndex:i] integerValue];
if (![self isMarked:temp]) {
[self depthSearch:graph vertex:temp];
}
}
}
-(Boolean)isMarked:(NSInteger)vertex{
return self.marked[vertex]==[NSNull null]?false:[self.marked[vertex] boolValue];
}
-(BOOL)stronglyConnected:(NSInteger)vertex otherVertex:(NSInteger)otherVertex{
return [self.ids[vertex] integerValue]==[self.ids[otherVertex] integerValue];
}
@end
测试代码:
Digraph *graph=[[Digraph alloc]initWithVertex:13];
[graph addEdges:4 endVertex:2];
[graph addEdges:2 endVertex:3];
[graph addEdges:3 endVertex:2];
[graph addEdges:6 endVertex:0];
[graph addEdges:0 endVertex:1];
[graph addEdges:2 endVertex:0];
[graph addEdges:11 endVertex:12];
[graph addEdges:12 endVertex:9];
[graph addEdges:9 endVertex:10];
[graph addEdges:9 endVertex:11];
[graph addEdges:8 endVertex:9];
[graph addEdges:10 endVertex:12];
[graph addEdges:11 endVertex:4];
[graph addEdges:4 endVertex:3];
[graph addEdges:3 endVertex:5];
[graph addEdges:7 endVertex:8];
[graph addEdges:8 endVertex:7];
[graph addEdges:5 endVertex:4];
[graph addEdges:0 endVertex:5];
[graph addEdges:6 endVertex:4];
[graph addEdges:6 endVertex:9];
[graph addEdges:7 endVertex:6];
KosarajuCC *graphCC=[[KosarajuCC alloc]initWithGraph:graph];
for (NSInteger i=0; i<graphCC.count; i++) {
NSMutableArray *dataSource=[[NSMutableArray alloc]initWithCapacity:1];
for (NSInteger j=0; j<graph.vertexs; j++) {
if ([graphCC.ids[j] integerValue]==i) {
[dataSource addObject:[NSNumber numberWithInteger:j]];
}
}
NSLog(@"分量%ld:%@",i,[dataSource componentsJoinedByString:@"--"]);
}
NSInteger vertex=0,otherVertex=1;
Boolean cc=[graphCC stronglyConnected:vertex otherVertex:otherVertex];
NSLog(@"节点%ld和节点%ld %@强连通的",vertex,otherVertex,cc==true?@"是":@"不是");
NSLog(@"技术交流群:%@",@"228407086");
NSLog(@"博客园-FlyElephant:http://www.cnblogs.com/xiaofeixiang");
测试结果:

标签:
原文地址:http://www.cnblogs.com/xiaofeixiang/p/4715319.html