标签:
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 4234 | Accepted: 1989 |
Description
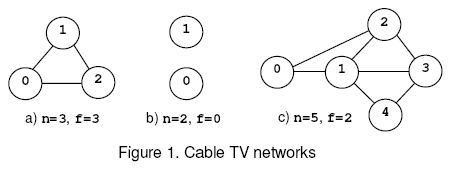
Input
Output
Sample Input
0 0 1 0 3 3 (0,1) (0,2) (1,2) 2 0 5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)
Sample Output
0 1 3 0 2
Hint
点连通度的定义:
一个具有N个点的图G中,在去掉任意k-1个顶点后(1<=k<=N),所得的子图仍然连通,去掉K个顶点后不连通,则称G是K连通图,
K称作图G的连通度,记作K(G)。
解决方法:构建网络流模型:
若G为无向图:
(1)原G图中的每个顶点V变成N网中的两个顶点 V` 和 V`` ,顶点V`至V``有一条弧容量为1;
(2)原图G中的每条边e=UV,在N网中有两条弧e` =U`` V` ,e``= V`` U` 与之对应,e`与e``容量均为无穷;
(3)以A`` 为源点,B` 为汇点,求最大流。
若G为有向图
(1)原G图中的每个顶点V变成N网中的两个顶点 V` 和 V`` ,顶点 V` 至 V`` 有一条容量为1的弧;
(2)原G图中的每条弧 e = U V 变成一条有向轨 U` U`` V` V`` ,其中轨上的弧 U`` V` 的容量为无穷;
(3)以A``为源点,B`为汇点求最大流。
上面的模型只求出了以A为源点B为汇点的最大流max_flow,等价于在G中只要去掉max_flow个点就会使得A与B不连通。而图的连通度是要求去掉最少的点使得整个图不连通,做法是枚举一个源点,另外枚举与源点不相邻的点为汇点,求最大流。在所有的枚举结果中最小的maxflow值就是要求的K(G).注意如果某次枚举的汇点求出 的最大流为无穷则说明此此枚举的源点与汇点是强连通的。如果所有的枚举结果都为无穷,则说明整个图G是强连通的,需要去掉n-1个点才能破坏其连通性。
边连通度:只许删边,求至少要删掉几条边。
构建一个网络N
若G为无向图:
1. 原G图中的每条边e=UV变成两条边e`=UV,e``=VU,容量都为1;
2. 枚举一个点为源点,再枚举与源点不相邻的为汇点,求最大流maxflow,保留最小的maxflow即为图的边连通度。
若G为有向图:
1. 原G图中每条有向边容量为1;
2. 此步骤与无向图的步骤2相同。
注意每次枚举源点,汇点找最小的maxflow时,需要把每条边的流量 edge[ i ] .flow清零 ,这点卡了我一晚上,一直wa。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#define INF 0x3f3f3f3f
#define maxn 1000+10
#define maxm 2000000+10
using namespace std;
struct node {
int u, v, cap, flow, next;
};
node edge[maxm];
int head[maxn], cur[maxn], cnt;
int dist[maxn], vis[maxn];
int n, m;
void init(){
cnt = 0;
memset(head, -1, sizeof(head));
}
void add(int u, int v, int w){
edge[cnt] = {u, v, w, 0, head[u]};
head[u] = cnt++;
edge[cnt] = {v, u, 0, 0, head[v]};
head[v] = cnt++;
}
bool BFS(int st, int ed){
queue<int>q;
memset(vis, 0, sizeof(vis));
memset(dist, -1, sizeof(dist));
vis[st] = 1;
dist[st] = 0;
q.push(st);
while(!q.empty()){
int u =q.front();
q.pop();
for(int i = head[u]; i != -1; i = edge[i].next){
node E = edge[i];
if(!vis[E.v] && E.cap > E.flow){
vis[E.v] = 1;
dist[E.v] = dist[u] + 1;
if(E.v == ed) return true;
q.push(E.v);
}
}
}
return false;
}
int DFS(int x, int ed, int a){
if(x == ed || a == 0)
return a;
int flow = 0, f;
for(int &i = cur[x]; i != -1; i = edge[i].next){
node &E = edge[i];
if(dist[E.v] == dist[x] + 1 && (f = DFS(E.v, ed, min(a, E.cap - E.flow))) > 0){
E.flow += f;
edge[i ^ 1].flow -= f;
a -= f;
flow += f;
if(a == 0) break;
}
}
return flow;
}
int maxflow(int st, int ed){
int flowsum = 0;
while(BFS(st, ed)){
memcpy(cur, head, sizeof(head));
flowsum += DFS(st, ed, INF);
}
return flowsum;
}
int main (){
while(scanf("%d%d", &n, &m) != EOF){
int u, v, mins;
init();
for(int i = 0; i < n; ++i)
add(i, i + n, 1);
while(m--){
scanf(" (%d,%d)", &u, &v);
add(u + n, v, INF);
add(v + n, u, INF);
}
mins = INF;
for(int i = 0; i < n; ++i)
for(int j = i + 1; j < n; ++j)
{
int sum = maxflow(i + n, j);
for(int i = 0; i < cnt; ++i){
edge[i].flow = 0;//每次找最大流时要把每条边的流量清零
}
mins = min(mins, sum);
}
if(mins >= n)
mins = n;
printf("%d\n", mins);
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
POJ 1966--Cable TV Network 【求无向图的点连通度 构造最大流模型 && dinic】
标签:
原文地址:http://blog.csdn.net/hpuhjh/article/details/47453453