“AS3.0高级动画编程”学习：第四章寻路（AStar/A星/A*）算法 (上)

时间：2015-08-14 15:40:20 阅读：265 评论：0 收藏：0 [点我收藏+]

标签：

一提到“A*算法”，可能很多人都有"如雷贯耳"的感觉。用最白话的语言来讲：把游戏中的某个角色放在一个网格环境中，并给定一个目标点和一些障碍物，如何让角色快速“绕过障碍物”找出通往目标点的路径。（如下图）

技术分享

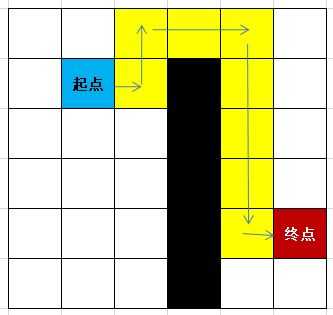
在寻路过程中，角色总是不停从一个格子移动到另一个相邻的格子，如果单纯从距离上讲，移动到与自身斜对角的格子走的距离要长一些，而移动到与自身水平或垂直方面平行的格子，则要近一些。为了描述这种区别，先引入二个概念：

节点(Node)：每个格子都可以称为节点。

代价(Cost)：描述角色移动到某个节点时所走的距离（或难易程度）。

技术分享

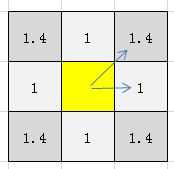
如上图，如果每水平或垂直方向移动相邻一个节点所花的代价记为1，则相邻对角节点的代码为1.4(即2的平方根--勾股定理)

通常寻路过程中的代价用f,g,h来表示

g代表(从指定节点到相邻)节点本身的代价--即上图中的1或1.4

h代表从指定节点到目标节点（根据不同的估价公式--后面会解释估价公式）估算出来的代价。

而 f = g + h 表示节点的总代价，为了方便后面的代码描述，这里把节点封装成一个类Node.as

 1 package {   
 2     public class Node
 3     {
 4         public var x:int;
 5         public var y:int;
 6         public var f:Number;
 7         public var g:Number;
 8         public var h:Number;
 9         public var walkable:Boolean=true;//是否可穿越（通常把障碍物节点设置为false）
10         public var parent:Node;
11         public var costMultiplier:Number=1.0;//代价因子
12  
13         public function Node(x:int, y:int)
14         {
15             this.x=x;
16             this.y=y;
17         }
18     }
19 }

View Code

注意：这里有二个新的东东walkable和parent。

通常障碍物本身也可以看成是由若干个不可通过的节点所组成，所以walkable实际上是用来标记该节点是否为障碍物(节点)。

另外：在考查从一个节点移动到另一个节点时，总是拿自身节点周围的8个相邻节点来说事儿，相对于周边的节点来讲，自身节点称为它们的父节点(parent).

前面一直在提“网格，网格”，干脆把它也封装成类Grid.as

 1 package
 2 {
 3  
 4     public class Grid
 5     {
 6         private var _startNode:Node;//开始节点
 7         private var _endNode:Node;//目标节点
 8         private var _nodes:Array;//节点数组
 9         private var _numCols:int;//列数
10         private var _numRows:int;//行数
11  
12         public function Grid(numCols:int, numRows:int)
13         {
14             _numCols=numCols;
15             _numRows=numRows;
16             _nodes=new Array();
17             for (var i:int=0; i < _numCols; i++)
18             {
19                 _nodes[i]=new Array();
20                 for (var j:int=0; j < _numRows; j++)
21                 {
22                     _nodes[i][j]=new Node(i, j);
23                 }
24             }
25         }
26  
27         public function getNode(x:int, y:int):Node
28         {
29             return _nodes[x][y] as Node;
30         }
31  
32  
33         public function setEndNode(x:int, y:int):void
34         {
35             _endNode=_nodes[x][y] as Node;
36         }
37  
38  
39         public function setStartNode(x:int, y:int):void
40         {
41             _startNode=_nodes[x][y] as Node;
42         }
43  
44  
45         public function setWalkable(x:int, y:int, value:Boolean):void
46         {
47             _nodes[x][y].walkable=value;
48         }
49  
50  
51         public function get endNode():Node
52         {
53             return _endNode;
54         }
55  
56  
57         public function get numCols():int
58         {
59             return _numCols;
60         }
61  
62  
63         public function get numRows():int
64         {
65             return _numRows;
66         }
67  
68  
69         public function get startNode():Node
70         {
71             return _startNode;
72         }
73     }
74 }

View Code

然而，在寻路的过程中“条条道路通罗马”，路径通常不止一条，只不过所花的代价不同而已

技术分享

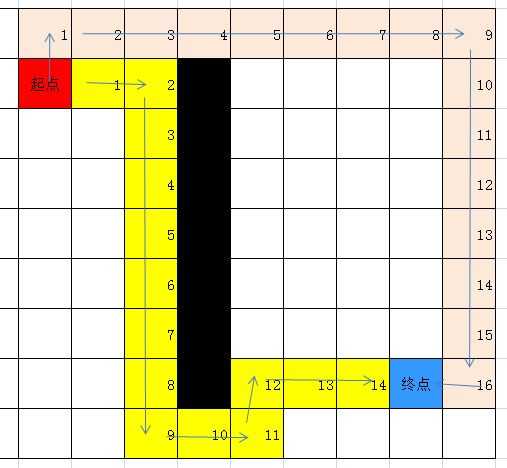
如上图，如果按照黄色路径走，所花的总代价是14，而按照粉红色路径走，所花的总代价是16，所以我们要做的事情，就是要尽最大努力找一条代价最小的路径。

但是，“好事总多磨”，即使是代价相同的最佳路径，也有可能出现不同的走法：

技术分享

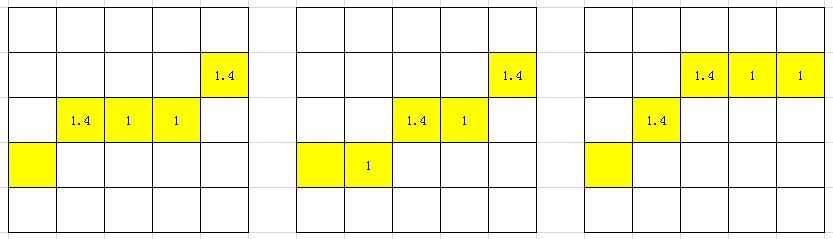
上图中三种不同的走法，总代价都是4.8，就上图而言，最佳路径(最小代价)用肉眼就能很快找出来，但是用代码如何估算起点与终点之间的代价呢？

 1 //曼哈顿估价法
 2 private function manhattan(node:Node):Number
 3 {
 4     return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y + _endNode.y) * _straightCost;
 5 }
 6  
 7 //几何估价法
 8 private function euclidian(node:Node):Number
 9 {
10     var dx:Number=node.x - _endNode.x;
11     var dy:Number=node.y - _endNode.y;
12     return Math.sqrt(dx * dx + dy * dy) * _straightCost;
13 }
14  
15 //对角线估价法
16 private function diagonal(node:Node):Number
17 {
18     var dx:Number=Math.abs(node.x - _endNode.x);
19     var dy:Number=Math.abs(node.y - _endNode.y);
20     var diag:Number=Math.min(dx, dy);
21     var straight:Number=dx + dy;
22     return _diagCost * diag + _straightCost * (straight - 2 * diag);
23 }

View Code

上面的代码给出了三种基本的估价算法(也称估价公式)，其算法示意图如下：

技术分享

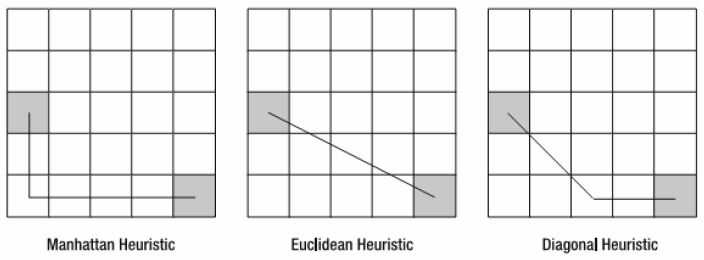
如上图，对于“曼哈顿算法”最贴切的描述莫过于孙燕姿唱过的那首成名曲“直来直往”，笔直的走，然后转个弯，再笔直的继续。

“几何算法”的最好解释就是“勾股定理”，算出起点与终点之间的直线距离，然后乘上代价因子。

“对角算法”综合了以上二种算法，先按对角线走，一直走到与终点水平或垂直平行后，再笔直的走。

我们可以针对刚才的情况做下测试：

 1 package
 2 {
 3     import flash.display.Sprite;
 4  
 5     public class GridTest extends Sprite
 6     {
 7         private var _endNode:Node;
 8         private var _startNode:Node;
 9         private var _straightCost:Number=1.0;
10         private var _diagCost:Number = 1.4;
11  
12  
13         public function GridTest()
14         {
15             var g:Grid=new Grid(5, 5);
16             g.setStartNode(0, 3);
17             g.setEndNode(4, 1);
18              
19             _endNode = g.endNode;
20             _startNode = g.startNode;
21              
22             var c1:Number = manhattan(_startNode);//8 
23             var c2:Number = euclidian(_startNode);//4.47213595499958
24             var c3:Number = diagonal(_startNode);//4.8
25              
26             trace(c1,c2,c3);
27         }
28  
29         //曼哈顿估价法
30         private function manhattan(node:Node):Number
31         {
32             return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y - _endNode.y) * _straightCost;
33         }
34  
35         //几何估价法
36         private function euclidian(node:Node):Number
37         {
38             var dx:Number=node.x - _endNode.x;
39             var dy:Number=node.y - _endNode.y;
40             return Math.sqrt(dx * dx + dy * dy) * _straightCost;
41         }
42  
43         //对角线估价法
44         private function diagonal(node:Node):Number
45         {
46             var dx:Number=Math.abs(node.x - _endNode.x);
47             var dy:Number=Math.abs(node.y - _endNode.y);
48             var diag:Number=Math.min(dx, dy);
49             var straight:Number=dx + dy;
50             return _diagCost * diag + _straightCost * (straight - 2 * diag);
51         }
52     }
53 }