标签:
/** function:
合并2个有序数组,有效到大
input:
数组first pData[begin..mid]
数组second pData[mid+1..end]
output:pData[begin...end]
需要空间:o(n)
**/
void merge(int *pData,int begin,int mid,int end)
{
int pTemp[8]={0};
int first =begin;
int second =mid+1;
int iTemp=begin;//iTemp开始位置不能每次都零开始,begin
while(first<=mid && second<=end)
{
if(pData[first]<=pData[second])
{
pTemp[iTemp++]=pData[first++];
}else
{
pTemp[iTemp++]=pData[second++];
}
}
//待排序数组 还没有剩余
while(first<=mid && second>end)
{
pTemp[iTemp++]=pData[first++];
}
while(second<=end && first>mid)
{
pTemp[iTemp++]=pData[second++];
}
for(int i=begin;i<=end;i++)
{
pData[i]=pTemp[i];
}
// delete []pTemp;
}
/***
function:非递归形式
统计i后门位置,比i小的个数,加入[0--i] 统计完毕之后,我是不计较后门是有些无需的
前提:自己没有统计完毕千万不打乱
1
如何做到间隔step访问 观察规律
根据step查分成n组
step=1
[0,1], [2,3] ,[4,5][6,7] begin
step=2;
[40,80] [20,60] begin 0 mid=1 end 3
[40,80] [20,60] ,[41,81] [21,61] begin 4 mid=5 end 7
step=4;
组后一组 可能少于一个step的数据
2 如何将一个step 数据排序完毕
**/
void merge_sort(int * pData,int length)
{
int step=0;//step 避免全部排序,为了判断是否第一我不要和每一个人打一架
int begin=0;//下一个拆分合并数组的开始位置
int mid=0;//begin-mid,mid-end 拆分需要合并的2个数组
int end =0;//待排序结束位置
//int temp[length]={0};//无法为temp申请空间 因为length不知道
//控制归并排序次数
for(step =1;step<length;step*=2)
{
cout<<"step=="<<step<<":"<<endl;
//控制一次归并排序,有多少对数字需要合并
//<=length必须等于 不如少计算一个数组
for(begin=0;(begin+2*step)<=length;begin=end+1)
{
mid=begin+step-1;
end=mid+step;
if(end>length-1)//第二个序列个数不足
{
end=length-1;
}
//cout<<"begin_mid__end:"<<begin<<"__"<<mid<<"__"<<end<<endl;
merge(pData,begin,mid,end);
//showData(pData,length);
}
showData(pData,length);
}
}
void testgetMaxSum()
{
int array[8]={0,5,-2,1,-8,7,6,-3};
showData(array,8);
merge_sort(array,8);
//showData(array,12);
}
输出结果:
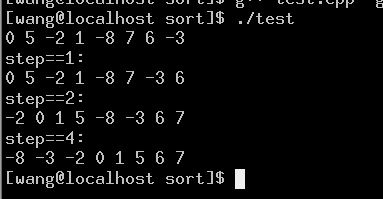
题目描述:
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
输入:
每个测试案例包括两行:
第一行包含一个整数n,表示数组中的元素个数。其中1 <= n <= 10^5。
第二行包含n个整数,每个数组均为int类型。
输出:
对应每个测试案例,输出一个整数,表示数组中的逆序对的总数。
样例输入:
4 7 5 6 4
样例输出:
5
【解题思路】
1 模拟人工计算方式 ,缺点 顺序执行
7 3
5 1
6 1
sum=3+1+1=5
缺点:N*N
2 如何上面联系起来。例如学生成绩比较 班级A和班级B,如果班级A 第一名(i) 大约班级B(i) 第一名
比较 ,就不需要和B中其他值比较了
标签:
原文地址:http://my.oschina.net/woyaoxue/blog/492924